TUSNDOKU
TUSNDOKUExperimentJLab HallA NIM PaperHIGH ACCURACY BEAM CURRENT MONITOR SYSTEM FOR CEBAF'S EXPERIMENTAL HALL AJLab Hall A BCMの昔?のページ The parametric current transformer, a beam current monitor developed for LEPDC current transformerの分かりやすい解説Modern and Future CollidersAbsolute calibration and monitoring of a spectrometric channel using a photomultiplerThe Aerogel Čerenkov detector for the SHMS magnetic spectrometer in Hall C at Jefferson LabPerformance of the Two Aerogel Cherenkov Detectors of the JLab Hall A Hadron SpectrometerシンチレータについてHeavy IonCollisions at and U+U Collisions at at STARNuclear ModelNijmegen PotentialsThe Nijmegen PotentialsExtended-soft-core baryon-baryon model ESC16. I. Nucleon-nucleon scatteringM. M. Nagels, Th. A. Rijken, and Y. Yamamoto, Phys. Rev. C 99, 044002 (2019)Extended-soft-core baryon-baryon model ESC16. II. Hyperon-nucleon interactionsSpectral Function and Momentum DistributionRealistic model of the nucleon spectral function in few- and many-nucleon systemsGround-state correlations and final state interactions in the process 3He(e,e′pp)nGround-state correlations and final-state interactions in exclusive lepton scattering off few-nucleon systemsTwo-nucleon correlations and the structure of the nucleon spectral function at high values of momentum and removal energyElectron and photon scattering on three-nucleon bound statesLimitations for the use of the spectral function in the semiexclusive 3He(e,e′N) processRealistic nucleon-nucleon interactions and the three-body electrodisintegration of 3HA Realistic Spectral Function of 4HeCalculations of the exclusive processes 2H(e,e′p)n,3He(e,e′p)2H, and 3He(e,e′p)(pn) within a generalized eikonal approximationElementary ProcessDifferentialcross sections for for and hyperonsTHE INTERACTION OF KAONS WITH NUCLEONS AND NUCLEI as a probe of partial deconfinement in nuclei-Nucleus Scattering and the "Swelling" of Nucleons in Nuclei total cross sections as a test for nucleon "swelling" total cross sections on and medium effects in nucleiQuasi Free Physics and Nuclear TransparencyUp and DownNeutron-neutron quasifree scattering in neutron-deutron breakup at 10 MeVMeasurement of Nuclear Transparency for the ReactionExperimental study of the reaction on and StrangenessQuasifree , , and electroproduction from , , and carbon Nuclear transparency and effective kaon-nucleon cross section from the reactionOptimal Fermi-averaging for the π++n→K++Λ t-matrix in Λ-hypernuclear production from (π+,K+) reactionsΛ-nucleon interaction in nuclei probed by the quasifree 12C(π+,K+) reactionMeson photo-production from Li, C, Al, and Cu nuclei at Photoproduction of mesons off nucleiNuclear mass number dependence of inclusice pion production by pions and protons at 4.3 GeV/cMeson-nucleaus potentials and the search for meson-nucleus bound statesFinal State InteractionFinal-state Lambda-neutron interaction in kaon photoproduction from the deuteronKaon photoproduction on the neutron using deuteriumMeson production in nucleon–nucleon collisions close to the thresholdLambda-neutron interaction in kaon photoproduction from the deuteronAnalysis of the ΛpΛp final-state interaction in the reaction p+p→K+(Λp)Λ Hypernuclei ReviewStrangeness in nuclear physics and studySearch for evidence of by observing and final states in the reaction of at 2A GeVResonances in the systemCan a Λnn Resonance Constrain the Λn Amplitude?Three-body resonances Λnn and ΛΛnΛnn bound state with three-body potentialIs there a bound ?Towards resolving the lifetime puzzleAnalysis of the Λ-Hypernuclear Three-Body SystemsBinding energies of the s-shell hypernuclei and the Λ well depthNon-existence of Λnn or Σ-nn bound statesLightest neutral hypernuclei with strangeness −1 and −2ΛNN and ΣNN systems at thresholdΛNN and ΣNN systems at threshold. II. The effect of D wavesThree-body hypernuclei in pionless effective field theoryInvestigation of the nnΛ bound state in pionless effective theoryStrange tribaryonsThree-body structure of the nnΛ system with ΛN−ΣN couplingA Λnn three-body resonanceProperties of the bound Λ(Σ)NN system and hyperon-nucleon interactionsDibaryonOn the history of dibaryons and their final observationCharge Symmetry BreakingObservation of the Hypernucleus by the Reaction Spectroscopy of the neutron-rich hypernucleus from electron scattering Double Charge ExchangeProduction of the Neutron-Rich Hypernucleus in the Double Charge-Exchange Reaction Missing-mass spectroscopy with the reaction to search for Repulsion and absorption of the Σ-nucleus potential for Σ−−5He in the 6Li(π−,K+) reactionSearch for hypernucleus by the reaction at Evidence for Heavy Hyperhydrogen First observation of the hyper superheavy hydrogen HypernucleiEvidence for a bound state of the Σ4 He hypernucleusObservation of a 4ΣHe Bound State in the 4He(K−,π−) Reaction at 600MeV/cCoulomb-assisted Σ−-nucleus bound states in the (K−,π+) reactionS = -2 physicsPossible Lightest Hypernucleus with Modern N InteractionKaonic NucleiN = 3 system Discovery of a strange tribaryon S0(3115) in 4He(stopped K−,p) reactionIndication of a strange tribaryon S^+ from the ^4He(stopped K^-,n) reactionSearch for strange tribaryon states in the inclusive 4He(Kstopped−,p) reactionSearch for strange tribaryons in the He4(Kstop−,nπ±) reactionStrange tribaryons as K¯-mediated dense nuclear systemsExotic HadronObservation of a Resonant Structure in Determination of the Lightest Strange Resonance or , from a Dispersive Data AnalysisMomentum dependence of the imaginary part of the - and - nucleus optical potentialNeutron-rich NucleiEvidence for the First Excited State of Nuclear StructureComparing proton momentum distributuions in A=2 and 3 nuclei via and measurementsSimulation TechniqueFSI and Quasi FreeDavid Gaskell D thethisBenjamin Clasie D thethisIncluding Fermi MotionMedium effects on Ξ− production in the nuclear (K−,K+) reactionOptimal approximation to elastic and inelastic scattering on a bound nucleon systemStatisticsStatistical Analysis in experimental particle physicsGoodness of fit tests for weighted histogramsOthersQuantum Measurements of Time量子力学(倉澤さん)A General Expression for Symmetry Factors of Feynman DiagramsIsobaric Analogue States
Experiment
JLab HallA NIM Paper
JLab Hall A NIM 論文
HIGH ACCURACY BEAM CURRENT MONITOR SYSTEM FOR CEBAF'S EXPERIMENTAL HALL A
JLab Hall A beam current monitorの論文
JLab Hall A BCMの昔?のページ
The parametric current transformer, a beam current monitor developed for LEP
JLab Hall A がbeam monitorのために採用しているPCMの原論文 。
DC current transformerの分かりやすい解説
Modern and Future Colliders
V. Shiltsev et al, arXiv:2003.09084
Absolute calibration and monitoring of a spectrometric channel using a photomultipler
E.H. Bellamy et al., NIM A 339, 3, 468-476 (1994)
PMTのキャリブレーション法について詳しい。基礎的な内容であるが、フィッティング関数など非常に参考になる。
The Aerogel Čerenkov detector for the SHMS magnetic spectrometer in Hall C at Jefferson Lab
T. Horn et al., Nucl. Ins. Method, Volume 842, 11, 2017, Pages 28-47
HALL CのAerogel Cherencov
Performance of the Two Aerogel Cherenkov Detectors of the JLab Hall A Hadron Spectrometer
S. Marrone et al., arXiv:0810.4630
HALL AのAerogel Cherencov
シンチレータについて
筑波大 飯田さん
Heavy Ion
Collisions at and U+U Collisions at at STAR
定番の重イオンdilepton測定。低い横運動量()でを測定。重イオンからのphoton生成とその相互作用に重点をおいている。photon-photon interactionはconducting QGP mediumにtrapされた強磁場の存在を探るプローブになり得る。 Fig1は、low でのee invariant massを示している。すべてのmass range, centralityでhadron cocktailで計算された値より超過がある。さらに、invariant mass,centrality dependenceが存在する。表面的な衝突60-80%の方がexcessが大きい。また、低いmass rangeでは、質量が増加するにつれてexessは減少していくが、φ質量を境に増加に転じ、周辺でmaxとなる。このふるまいの違いは異なるprocessに起因すると予想される。 regionに関しては解析中であり、今回は、について。 Fig2はcentrality 60-80 %での依存性。のみにexessがみられる。では、超過は見られず、hadron cocktailでよく説明がつく。 Fig3は、low を抜き出し、さらにinclusive ee pairsを引いた(何で?)状態でのinvariant mass distribution。(a)はcentrality 40-60 %, (b)はcentrality 60-80 %。理論計算は、in-medium broadened modelとQGP radistionを含んでいる。この理論は、high で実験されているSPSとRHICのdataを説明したが、本データを説明できなかった。(low centralityでは説明できているのかどうか知りたい) さらに、この状態でのexessのcentrality依存性を示したのがFig3.c。このevent selectionではほとんどcentrality依存性がない。一方で、hadron cocktailでの計算結果はcentrality依存性を示している。これは、ハドロン相互作用ではこのee pairs exessを説明できないことを示している(こういってしまって大丈夫なのか?broadend とQGP radiationでは説明できないということが分かっただけなのでは?)。 low ee enhancementの起源を調べるため、実験データをphotonuclearとphoton-pthonの寄与を考慮したmodelと比較した。このmodelにも二種類あり、ZhaによるものとSTARlight MCによるものがある。これらの違いはphton fluxを見積もる際に原子核の電荷分布を考慮するかどうかなどがあるが、ともに仮想光子生成に対するハドロン相互作用の考慮はしていない。これらの理論を用いるとデータを良く再現できる。ただし、centrality60-80 %ではSTARlightは少しunderestimateしている。結果からphotonuclear effectは無視できると分かった。 はしんどくなったからまだ読んでない
Nuclear Model
Nijmegen Potentials
The Nijmegen Potentials
J.J. de Swart, R.A.M.M. Klomp, M.C.M. Rentmeester, ThA. Rijken, arXiv:nucl-th/950924
Extended-soft-core baryon-baryon model ESC16. I. Nucleon-nucleon scattering
M. M. Nagels, Th. A. Rijken, and Y. Yamamoto, Phys. Rev. C 99, 044002 (2019)
Extended-soft-core baryon-baryon model ESC16. II. Hyperon-nucleon interactions
M. M. Nagels, Th. A. Rijken, and Y. Yamamoto, Phys. Rev. C 99, 044003 (2019)
Spectral Function and Momentum Distribution
Realistic model of the nucleon spectral function in few- and many-nucleon systems
C. Ciofi degli Atti and S. Simula, Phys. Rev. C 53, 1689 – Published 1 April 1996
Ground-state correlations and final state interactions in the process 3He(e,e′pp)n
C. Ciofi degli Atti and L. P. Kaptari, Phys. Rev. C 66, 044004 – Published 17 October 2002
Ground-state correlations and final-state interactions in exclusive lepton scattering off few-nucleon systems
C. Ciofi degli Atti, L.O. Kaptari, Nuclear Physics A, Volume 699, Issues 1-2, 25, Feburuary 2002, Pages 49-56
Two-nucleon correlations and the structure of the nucleon spectral function at high values of momentum and removal energy
C. Ciofi degli Atti, S. Simula, L. L. Frankfurt, and M. I. Strikman, Phys. Rev. C 44, R7(R) – Published 1 July 1991
Electron and photon scattering on three-nucleon bound states
J. Glokak, et al, Physics Reports, Volume 415, Issues2-3, Pages89-205
Limitations for the use of the spectral function in the semiexclusive 3He(e,e′N) process
J. Golak, H. Witała, R. Skibiński, W. Glöckle, A. Nogga, and H. Kamada, Phys. Rev. C 70, 034005 – Published 28 September 2004
Realistic nucleon-nucleon interactions and the three-body electrodisintegration of 3H
C. Ciofi degli Atti, E. Pace, and G. Salmè, Phys. Rev. C 21, 805 – Published 1 March 1980
A Realistic Spectral Function of 4He
H. Morita, T. Suzuki Prog. Theor . Phys. 86 671
Calculations of the exclusive processes 2H(e,e′p)n,3He(e,e′p)2H, and 3He(e,e′p)(pn) within a generalized eikonal approximation
C. Ciofi degli Atti and L. P. Kaptari, Phys. Rev. C 71, 024005 (2005)
Elementary Process
Differentialcross sections for for and hyperons
R. Bradford et al., Phys. Rev. C 73, 035202 (2006)
THE INTERACTION OF KAONS WITH NUCLEONS AND NUCLEI
Carl B. Dover, George E. Walker, Phys. Rep. 89, 1-177 (1982)
散乱 Nucleon散乱について徹底的に調べている。、 Nucleonも詳しい。
as a probe of partial deconfinement in nuclei
R. B. Siegel, W. B. Kaufmann, and W. R. Gibbs, Phys. Rev. C 31, 2184 (1985)
N 散乱の情報を使って- Nucleon散乱の断面積を理論的に計算。従来のみの原子核の理解のみでは- Nucleon散乱を説明できないことを示した。しかし、- Nucleon散乱は、仮にが原子核中で10 %拡がっていいれば(swelling)説明できると計算。
-Nucleus Scattering and the "Swelling" of Nucleons in Nuclei
G. E. Brown, C. B. Dover, P. B. Siegel, and W. Weise, Phys. Rev. Lett. 60, 2723 (1988)
mesonが軽くなれば説明のつかない- Nucleon 散乱を説明できると計算。低エネルギーN 散乱は channel が支配的。これはI=1, S=1ボソン交換を意味し、 meson交換を意味する
total cross sections as a test for nucleon "swelling"
Y. Mardor et al., Phys. Rev. Lett. 65, 2110 (1990)
BNLで- Nucleon散乱を測定。上のSiegelとBrownの理論計算と比較した。結果から、従来の原子核理論では説明がつかないこと、さらにSeigelとBrownに近いことが分かった。二つの理論の内では、Siegelの方が近い。といってもびったりあっているわけではない。
total cross sections on and medium effects in nuclei
R. A. Krauss et al., Phys. Rev. C 46, 655 (1992)
上のBNLの実験結果をさらにデータ取得+解析。やはり従来とは説明がつかないが、Sewllingの効果とは言い切れない。より詳細な研究が重要。
Quasi Free Physics and Nuclear Transparency
Up and Down
Neutron-neutron quasifree scattering in neutron-deutron breakup at 10 MeV
R. C. Malone et al., Phys. Rev. C. 101, 034002 (2020)
Measurement of Nuclear Transparency for the Reaction
Experimental study of the reaction on and
Strangeness
Quasifree , , and electroproduction from , , and carbon
INTRODUCTION のQuasi free electro productionを調べた。Neutron targetを使用することはできないので、やを用いて中性子の情報を抜き出すことが多い。質量数Aが増加するとFermi motionが大きくなってくるため、中性子の効果を抜き出すことは難しくなる。 また、異なる質量数の原子核を系統的に調べることで、Elementary kaon electroproductionのin-medium modificationを調べることも期待される。実際に、を用いた実験で理論と一致しない結果が得られている。 この論文では、のQuasi free electro productionの断面積を報告する。特に、に対しては初めての結果である。
EXPERIMENT
JLab Hall C で行われた実験。電子エネルギーはで、標的厚さは、標的長は4 cm。
使用されたスペクトロメータはHMS(for scattered electrons, momentum acceptance , ) とSOS(for kaon, momentum acceptance, )。HMSの角度は14.93°に固定されており、すなわちVP Fluxは一定。Virtual photonは、。一方、SOSの角度は最初13.4°でそこから変化させる。これは に対応する。運動量の中心値は、1.57 GeV(electron), 1.29 GeV(kaon)。
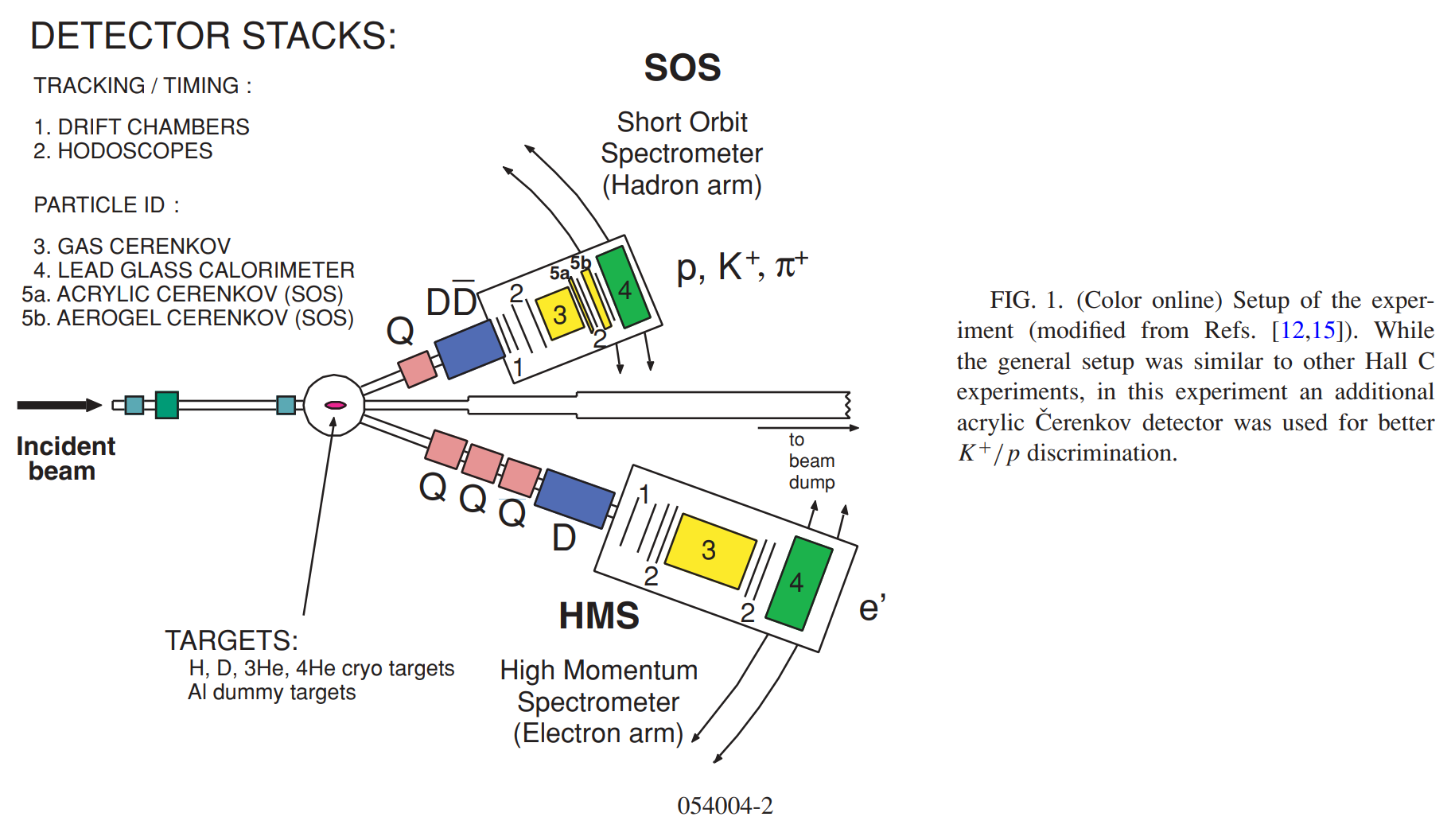
DATA ANALYSIS
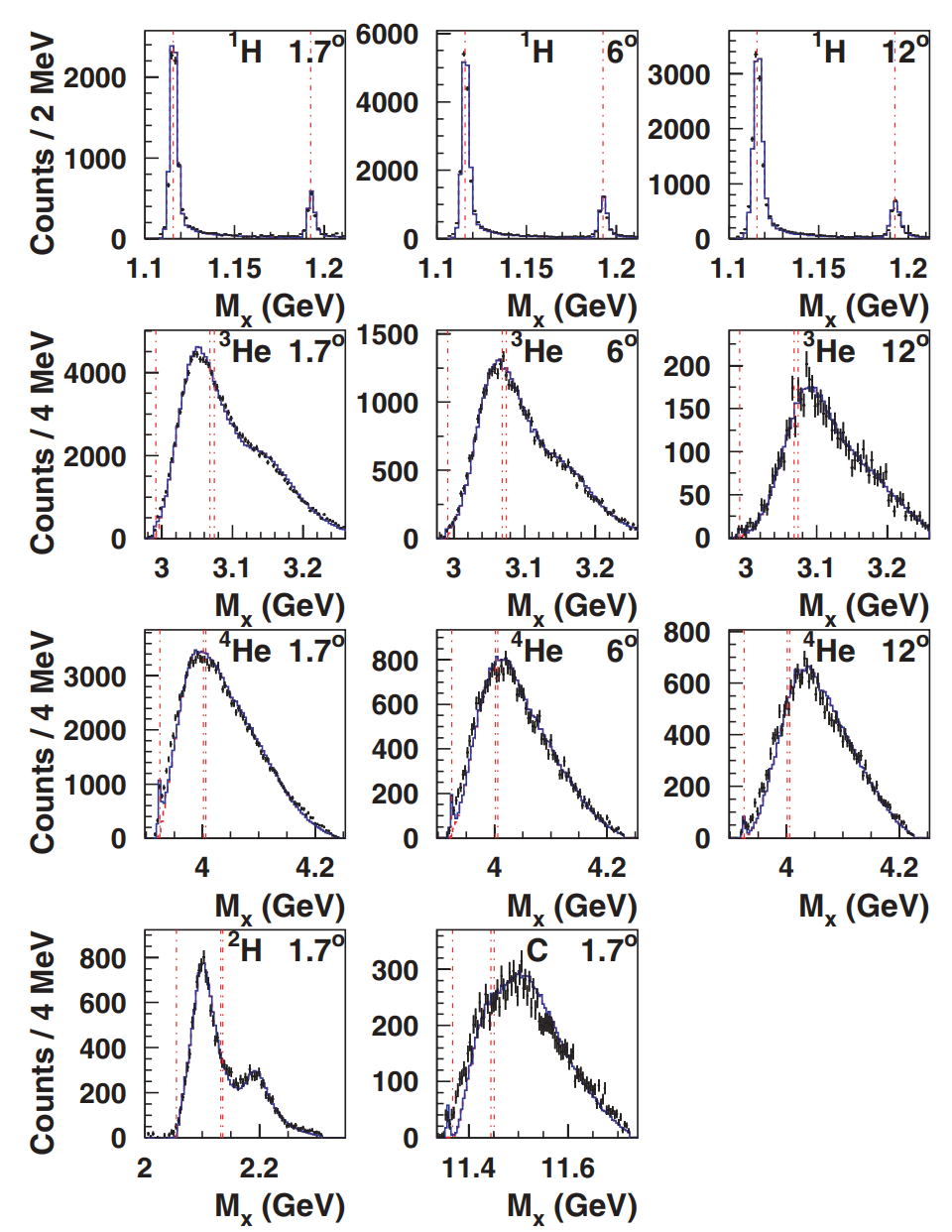 上図はそれぞれの標的に関するMissing Massであり、BGは既に引いている。Hに関して、Missing MassのAccuracyは2 MeVより良い。質量数Aが増加するにつれてΛとΣの分離が難しくなっている。
以下では、Monte Carlo Simulationを使用して、これらのMissing Massを, , , の3つの反応に分離することを試みる。VP Flux を既知とすると、反応断面積はと表される。このを考えていく。
上図はそれぞれの標的に関するMissing Massであり、BGは既に引いている。Hに関して、Missing MassのAccuracyは2 MeVより良い。質量数Aが増加するにつれてΛとΣの分離が難しくなっている。
以下では、Monte Carlo Simulationを使用して、これらのMissing Massを, , , の3つの反応に分離することを試みる。VP Flux を既知とすると、反応断面積はと表される。このを考えていく。
Modeling Hydrogen target このデータは規格化、isobar modelのテスト等に用いる。Saclay-Lyon modelが良く実験を再現することが分かっているが、"dedicated simple model"の方が実験をより再現する。
このモデルでは、は以下の式で表される。
ここで、
cはfitによって決められるパラメータ。観測された依存性はとても弱く、定数とおいている。W依存性はphase space factorとBreit-Wigner resonanceで構成されている。t依存性はBrauelによって決定された。依存性はChaによって調べられた結果である。
次にについて。これはエネルギーに依存したphase space factorを表す一項で表す。はKoltenukによって決定されている。
Except for Hydrogen target とを分けることはできないため、proton 標的に関してはとの生成比は hydrogen target と変わらないという仮定を置く必要がある。それぞれの断面積は、上述の hydrogen target に対する式に陽子数 Z と中性子数 N をかけたものを用いた。これらの式にさらに spectral function を畳み込んでシミュレーションを行った。 spectral function は標的中核子の四元運動量分布を与える。A = 2では、Bonn potential に基づく運動量分布とAv18に基づく運動量分布はほとんど一致する。これらのモデル自身は in-medium 効果や FSI を取り込んでいない。
Final State Interaction ΛN interaction は interactionより二桁大きいと考えられているため、FSIを考慮する必要がある。このために、Effective range approximation (ERA) を用いた。ERAでは断面積を enhancement factor I で修正する。
ここで、は l 次の Jost functionであり、はハイペロンと核子の相対運動量。YN potential Vはs波成分のみを使用した。s波の Jost function は以下で表される。
とは YN potential の散乱長aと有効長を用いて以下のように表られる。
以上の過程には free parameter が含まれない。散乱長と有効長は YN potential から決定される。potential としては Nijmegen potential を用いた。これは、 標的には良い結果を与えるが、deuteron には良い結果を与えなかった。従って、deuteron に対しては異なる方法で enhancement factor I を求めERAを行った。その方法は以下の通りである。Bethe formulaによって求めた s 波 phase shift を求め、enhancement factor I を以下の式で導いた。
FSI を考慮に入れた結果、 FSI の方が FSI よりも大きな影響を及ぼすことが分かった。
Extraction of Cross Section Hydrogen target H target に対しては、それぞれの kinematics 毎に以下の関数でデータを fit して2つの parameter とを決定する。
さらに fit parameter の比を以下のように定義する。
Except for hydrogen target A = 2 以上の標的ではが含まれてくるため、上記の式に修正が必要である。
このは FSI を含んでいる。これをフィッティングする際、とを分離できないため、もう一つ仮定を置く必要がある。本解析では、proton 由来のとの生成比はAに依存しないとする。つまり、
この仮定によりは free parameter ではなくなる。さらに 標的に関しては束縛が見えているため、もう一つパラメータを追加して束縛領域を表現した。
RESULTS AND DISCUSSION との断面積を計算した。どちらの標的においてもは大きな角度で断面積が落ちており、は角度に依存していない。はでは flatであり、では大きな角度で断面積が落ちている。 また、 Monte Carlo と data の比較において、 閾値近傍が一致していない。これは、ERA だけでは FSI が表現できていないためだと考えられる。
Nuclear transparency and effective kaon-nucleon cross section from the reaction
Optimal Fermi-averaging for the π++n→K++Λ t-matrix in Λ-hypernuclear production from (π+,K+) reactions
Toru Harada, Yoshiharu Hirabayashi, 744, 323-343 (2004)
Λ-nucleon interaction in nuclei probed by the quasifree 12C(π+,K+) reaction
T. Kishimoto et al, Phys. Rev. C 51, 2233 (1995)
Meson
photo-production from Li, C, Al, and Cu nuclei at
T. Ishikawa et al., Phys. Let. B 608 p215 (2005)
Photoproduction of mesons off nuclei
B. Krusche, The European Physical Journal, 198, 199 (2011)
Nuclear mass number dependence of inclusice pion production by pions and protons at 4.3 GeV/c
M. Ono et. al., Physics Letters, 84B 4 (1079)
Meson-nucleaus potentials and the search for meson-nucleus bound states
V. Metag et al, Progress in Particle and Nuclear Physics, Volume 97, 199-260 (2017)
Final State Interaction
Final-state Lambda-neutron interaction in kaon photoproduction from the deuteron
Xiaodong Li and L E Wright, Journal of Physics G: Nuclear and Particle Physics, 17, 7 (1991)
Kaon photoproduction on the neutron using deuterium
Xiaodong Li, L. E. Wright, and C. Bennhold, Phys. Rev. C 45, 2011 (1992)
Meson production in nucleon–nucleon collisions close to the threshold
C. Hanhart, Phys. Rep, 397, 3-4, (2004) 155-256
Lambda-neutron interaction in kaon photoproduction from the deuteron
R. A. Adelseck and L. E. Wright, Phys. Rev. C 39, 580 (1989)
Analysis of the ΛpΛp final-state interaction in the reaction p+p→K+(Λp)
F. Hinterberger and A. Sibirtsev, The European Physical Journal A, 21, 313-321 (2004)
Λ Hypernuclei
Review
Strangeness in nuclear physics
A. Gal, E. V. Hungerford, and D. J. Millener, Rev. Mod. Phys. 88, 035004 (2016)
and study
Search for evidence of by observing and final states in the reaction of at 2A GeV
C. Rappold et al. (Hyp HI Collaboration), Phys. Rev. C 88, 041001 (2013)
Resonances in the system
Iraj R. Afnan and Benjamin F. Gibson, Phys. Rev. C 92, 054608 (2015)
ファデーエフ計算を用いて、 共鳴状態の存否を調べた。 相互作用は 散乱長と有効長にあわせた。ポテンシャルとして、 rank-one separable potential、特にrank-one Yamaguchi potential (原論文は1954 年と大分古い) を用いた。これはとの散乱長と有効長をfitするためによく用いられる。形は以下のようになっている、
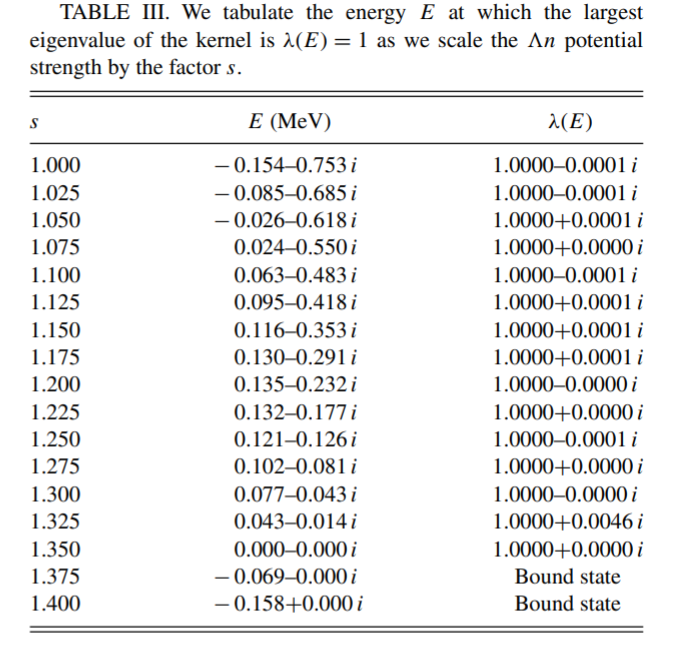
ここでCはポテンシャルの強さ、はポテンシャルのレンジ。この二つの量はバリオン相互作用モデルの散乱長と有効長の値から求めることが出来る。この計算では、とは束縛しない。これをhyper tritionに応用した場合でも概ね一致した。そこで、この計算を に適用したところ、固有値は となった。しかし、 であるので、共鳴ではない。そこで、 potential の をそれぞれ s 倍スケールして、energy plane上の軌道を確かめた。それが下図。わずか7 %強くすれば共鳴状態が生じる。さらに 35 %強くすれば束縛状態が生じる。しかし、束縛状態での散乱長、有効長を考慮すると、これはCSBを無視すれば散乱実験で否定されているように見える。しかし、 に対する実験データが不足しているため、明確な結論は下せない。
また、試しにテンソル力を含めた 相互作用を用いたものでも計算を行った。すると、結果は であった。この時、5 %強くすれば共鳴、25 %強くすれば束縛が生じることが分かる。
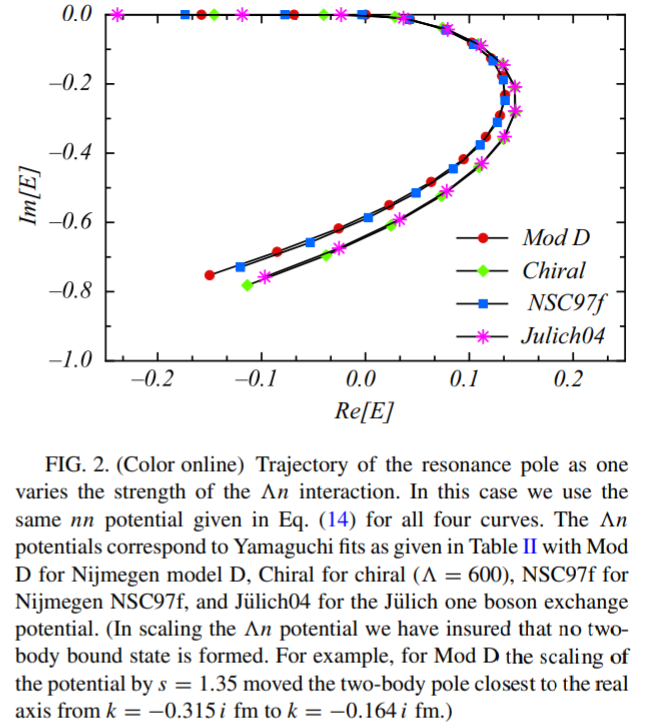
さらに他の様々なバリオン間モデルを用いた計算も行った。以前と同様にそれぞれのモデルの散乱長、有効長を用いて yamaguchi potential のパラメータを決定した。それらの結果が下図。用いた理論は、 Nijegen model D, Chiral model, Julich04 , Nijmegen NSC 97f である。全てのmodel において軌道はほとんど一致している。

より明確な結論を出すためには、より現実に近い相互作用、例えばテンソル力、 coupling、三体力を考慮する必要がある。
Can a Λnn Resonance Constrain the Λn Amplitude?
Iraj R. Afnan, Benjamin F. Gibson, Few-Body Systems 60 51 (2019)
Three-body resonances Λnn and ΛΛn
V. B. Belyaev, S. A. Rakityansky, W. Sandhas, Nucl. Phys. A, 803, 3-4 (2008), 210-226
と 系の共鳴と束縛を調べた。hyperspherical harmonics を用いて、三体ヨスト関数のゼロ点を探した。計算の結果、 の束縛は存在しないが、2 MeV 以上の幅の広い共鳴が存在するとなった。さらに、束縛するためには scaling factorを1.5 以上にする必要があることが分かった。これは Yamaguchi potentialを用いたAfnan と Gibson の論文の約二倍の値である。
と ポテンシャルは現存のハイパー核の束縛状態と合うように決定される。なぜなら、 粒子の散乱実験は難しいからである。しかし、仮に散乱実験が十分であっても、相互作用を一意に決定することが出来ないことが良く知られている [7]。つまり、異なるが phase-eauivalent なポテンシャルを作ることができる。したがって、異なるポテンシャルがハイパー核のスペクトルを説明してしまうことがあり得る。少数の 散乱データがあるとはいえ、より精密な 相互作用の理解にはさらに別の手法が必要である。有力な候補が 共鳴の研究である。散乱や束縛が主に on-shell での性質の現れであるのに対し、共鳴は off-shell の効果 (phase-eauivalent が異なる)が強く現れる[10],[11]。
と は二体 ( ) で結合しないため、考え得る散乱過程は のみである。散乱状態の波動関数は入ってくる超球面波と出ていく超球面波の重ね合わせであるため、三体を超球面座標で表すと便利である。凍時、波動関数は無限個の超級調和関数で展開される (二体波動関数が部分波に展開されるのと同じ) 。さらに と は量子数の都合上同じ方程式で扱うことが出来る。
計算を行うために二体相互作用が必要であるが、これは Nemura らの計算 (Minesota potential) を使用した。三体計算は異なる超角運動量の無限個の重ね合わせであるが、簡単のために hypercentral approximation (minimal approximation) (二体問題でいうところの S 波近似) を行う。この結果、二体問題と同じ方程式を得ることができる (ただし、l は整数ではない)。その結果が下図である。A,B,C は Nemura らによって提示された三つの 相互作用についてそれぞれ計算したものである。また、 では 相互作用についても Nemuraらに提案されたものとは違うものも試している。その状態で前述の 相互作用を試したものを としている。これらを用いて三体ヨスト関数の解を数値的に求めた。
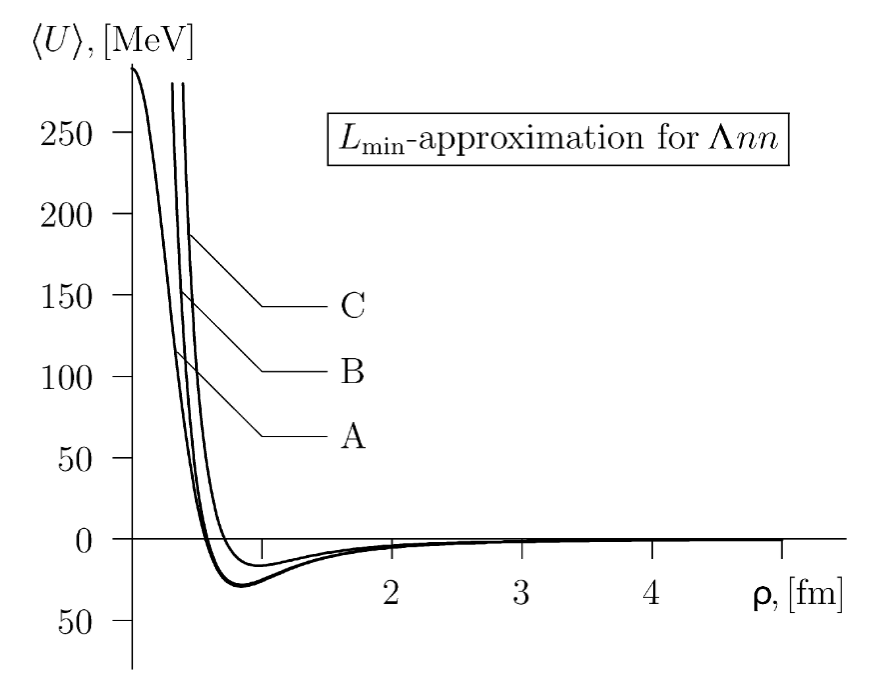
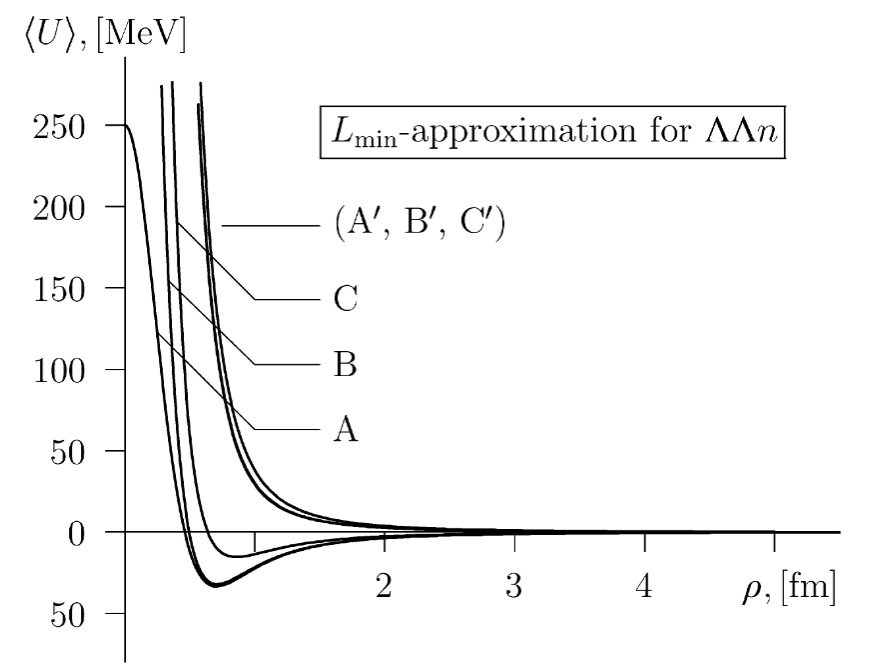
結果、実の負エネルギー状態に 0 は見つからなかった。つまり、 と に束縛状態は見つからなかった。 に関しては、共鳴領域に 0 が見つかった。しかし、これは 相互作用の取り入れ方に強く依存する。下のテーブル4 はその結果であり、A, B では共鳴があるが、C ではない。に関しては 相互作用がより重要であることが分かった。まず、 Nemuraらによって提案された 相互作用を用いた計算では、テーブル 5 のようにA, B では共鳴が見つかり、 C では共鳴がなかった。しかし、この 相互作用では が束縛しすぎてしまうことが分かっている。従って、さらにより現実的な 相互作用モデルも用いてみた。その結果が上のポテンシャル図の である。図から分かるように引力領域が存在せず、従って束縛も共鳴も存在しない。さらに、 状態に関してどうすれば束縛が生じるのかを調べた。図のポテンシャルの深さを手でスケールしてみたところ、ポテンシャルの強さを約 50 % 深くすれば束縛が生じることが分かった。

が より束縛しにくいことは自然に理解できる。なぜなら、 では であるのに対して、 では であり、 は よりも弱いからである。今回の研究は見積もり程度のものであるが、閾値近辺に共鳴がありそうなのは明らかである。さらに conversion を取り入れれば、引力はさらに強くなり、共鳴幅ももっと細くなるだろう。上に述べたように、この共鳴状態は二体相互作用に強く依存する。仮に共鳴状態が観測されれば YN, YY ポテンシャルに対する重要な情報を与えることができるだろう。
Λnn bound state with three-body potential
Igor Filikhin, Vladimir Suslov and Branislav Vlahovic, EPJ Web of Conferences 113, 08006 (2016)
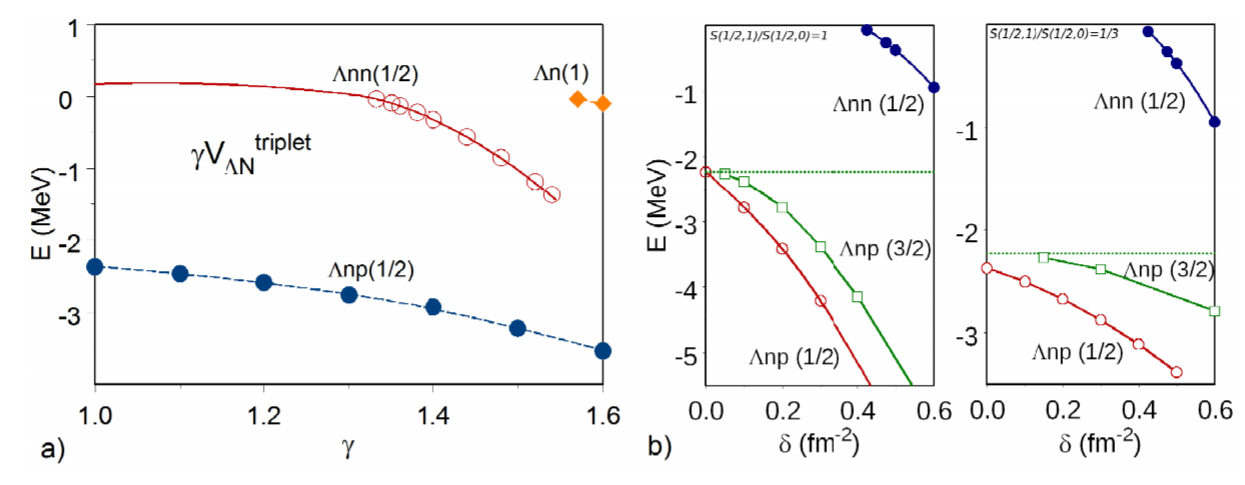
configuration-space ファデーエフ方程式を用いて の束縛・共鳴を調べた。特に GSI で発見された を説明するために spin-dependent 三体ポテンシャルを導入したのが特徴である。 相互作用には NSC97f を、 には MT-I-III model を用いた。まずはこれらの二体相互作用のみで計算を行った。このモデルはハイパートライトンの束縛エネルギーを 140 keV と良く再現できる。また、アイソスピン依存性を取り入れるために係数 を取り入れた。これは 相互作用の triplet 成分を scale するものである。まず、 状態で調べたところ、 に幅の広い共鳴を見つけた。共鳴エネルギーは 0.2 MeV であった。 これは Belyaev らの計算結果と一致する。
さらに、今回のモデルでは、三体 ポテンシャルをハミルトニアンの摂動として取り入れられていることとした。具体的な形は以下のようである。
ここで、 は hyper-radius: ( は Jacobi 座標系) であり、関数 S はハイペロンのスピン とNN pair のスピン のスピンに依存する。さらに二つのフリーパラメータ は調整する。
結果が下図である。左図は三体力を取り入れない状態での束縛エネルギーである。横軸は ポテンシャルの triplet 成分を scale するパラメータである。右図は、三体力を取り入れた結果である。左右ではスピン依存性が異なる。左は としたとき、右は としたときのものである。 束縛状態を説明するようにパラメータを調整した結果、ハイパートライトンが束縛しすぎてしまうことが分かった。スピン依存の ポテンシャルを新たに取り入れたが、これでもハイパートライトンを過束縛せず、 を束縛させることはできなかった。三体力を取り入れた状態でも (実はいれていない?本文からは読み取れない) の共鳴はあり、エネルギーは 0.2 MeV、幅は 2 MeV であった。
Is there a bound ?
Avraham Gal, Humberto Garcilazo et al, Phys. Lett B 736 (2014) 93 - 97
様々なハイパー核、特に A = 4 体系から の束縛状態に対する制限を課した。計算の際には coupling の効果も取り入れた。
まず、 と 散乱を比較する。低エネルギーYN 散乱から決められた YN potential を用いて YNN ファデーエフ方程式を解いた。これは Garcilazo (1987) の方法である。単純化のために、 散乱のスピン依存性は無視した。 effective range としては二つの値を試した。これらを用いて、 T = 0, T =1 の 系 がそれぞれそくばくするのに必要な散乱長 a 、さらにその時の断面積を求めた。結果が下図の通りである。実験結果は であり、予想通り、 の時に最も値が近くなる。一方で、 が束縛するようにすると、断面積が非常に大きく、さらにハイパートライトンの束縛も非常に深くなってしまう。

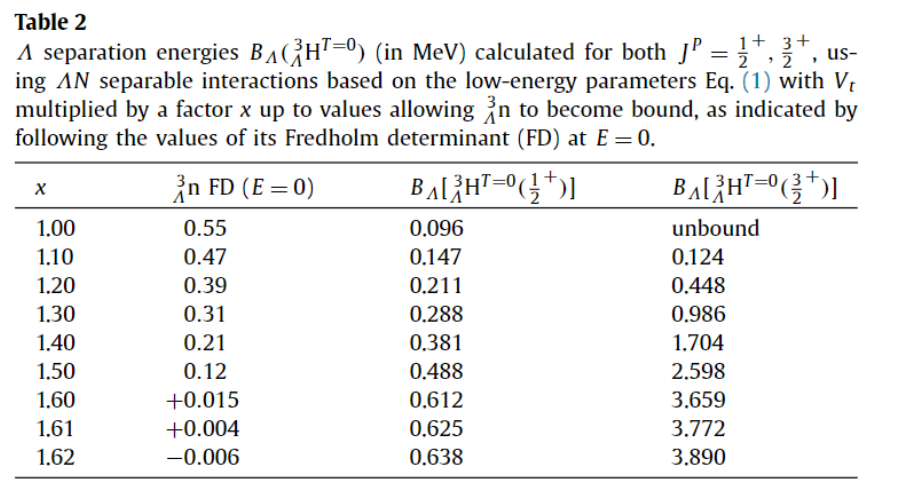
次に と を比較する。この節では s 波の 有効相互作用のみを考える。前節と同様に YNN 三体系のファデーエフ方程式を解く。 Nijimegen の四つのポテンシャルの内、ハイパートライトンの基底状態を説明できるモデル B を用いる。しかし、このポテンシャルは 3/2+ 状態を基底状態のわずか 11 keV 上に予想してしまうので、インプットパラメータを調整した。この状態で、 相互作用の triplet 成分を手でスケールして各々の状態がどのように変化するのかを見た。それが下図。 x が triplet を調整するパラメータであり、 1.00 が通常の状態。triplet 成分を上げていくと、 が基底状態になることが分かる。これは、 1/2+ がのポテンシャルが と表されるのに対して、 3/2+ のポテンシャルが と表されるため、 triplet 成分がより効いてくるためである。 x = 1.614 の時、 状態が束縛するが、この時、ハイパートライトンの束縛エネルギーは 2.76 MeV と非常に深い。この結果は前節のスピンに依存していない解析ともおおむね一致する。
次に と を比較する。ハイパー核の束縛エネルギーを考える際に coupling を無視することはできない。 one - pion 交換は channel 間の結合を強くする。これはハイパートライトンの三体計算において の項を支配する。 一方で、 channel においては coupling の効果は弱い。 ここでは、 の有効相互作用を G-matrix 計算で用いる。この相互作用はスピン依存の中心力である。
ここで、 はアイソスピン空間 を に変換する演算子である。これらのパラメータは NSC97e によって決定する。下図の下二行は、 conversion の束縛エネルギーへの寄与である。 A = 4 体系を考えると、 conversion は実測値 1.1 MeV の約半分を担っていることが分かる。A = 3 体系ではハイパートライトンの束縛が弱い(核子間の距離が大きい)のでこの効果は幾分か弱くなると考えられるが、それでも が束縛しないと考えるのは自然である。 次に を考える。まず、SU(4) 対称性を考える(pp, nn, pn, npが縮退?)。すると、A = 4 体系と比べて、A =3 体系の conversion が抑制されていることを で表すと、
と書ける。これを最大にするようにパラメータを設定すると、 の dineutron からの束縛エネルギーは 0.39 MeV となる。次に、 系のファデーエフ方程式を解き、 、 となるように スピン相互作用を決定した (SU(4)では deuteron と dineutron は同じ)。この時、散乱長は -1.804 fmであった。nn 相互作用に関しては となるように決めた。この時、 となった。さらに、次の計算として、この 相互作用は保ったまま、 SU(4) を破る形で NN 相互作用を変えて、現実の unbound dineutron の値である、 を参考にして を調節していった。その結果が table4 である。結果として、 dineutron よりも先に が束縛しなくなってしまうことが分かった。


Towards resolving the lifetime puzzle
A. Gal, H. Garcilazo, Phys. Lett. B 791 48-53 (2019)
Analysis of the Λ-Hypernuclear Three-Body Systems
B. W. Downs and R. H. Dalitz, Phys. Rev. 114, 593 (1959)
Binding energies of the s-shell hypernuclei and the Λ well depth
A. R. Bodmer, Q. N. Usami, Nucl. Phys. A , 22 621-651 (1988)
Non-existence of Λnn or Σ-nn bound states
H. Garcilazo, Journal of Physics G, 13, 5 (1987)
Lightest neutral hypernuclei with strangeness −1 and −2
Jean-Marc Richard, Qian Wang, and Qiang Zhao, Phys. Rev. C 91, 014003 (2015)
の存在は 同位体の安定性から 提案されていたが、示唆する実験は一つしかなく、それもまだ議論の余地がある。理論的にも現実的な nn 相互作用での束縛は難しく、パウリ排他律のために束縛は難しいと考えられる。一方で、 はパウリ排他律の影響をうけないため、その存在を考える余地はある。 や はエフィモフ状態になる可能性があり、それを調べてみることも面白い。Fig1からわかるように、三体系よりも四体系の方が許されるパラメータ空間が広いため、エフィモフ状態の希望がある。
計算手法として、 efficient variational method を用いた。 結果、deuteron とハイパートライトンは束縛したが、 ハイパートライトンの I = 1 の状態と 状態は束縛しなかった。一方で、I = 0 の は Nijmegen-RIKEN model では 約 3 MeV の弱い束縛、CEFT では 9 MeV 閾値より上、という結果であった。I = 1 の では、 Nijmegen-RIKEN model はパラメータが少ないため、うまく計算が出来なかったが、CEFT では 1 MeV の束縛となった。しかし、現在は三体力の効果を入れていないため、確実な結論を下すことは出来ない。さらに次の節では による の生成について述べている(省略)。
ΛNN and ΣNN systems at threshold
H. Garcilazo, T. Fernández-Caramés, and A. Valcarce, Phys. Rev. C 75, 034002 (2007)
構成子クォークモデルを用いて作った三体方程式を厳密に説いた。と の結合が の束縛に重要であり、 が系 で唯一の束縛状態であるという結果を得た。しかし、三体共鳴を考慮していないと Belyaev らの論文で指摘されている。
ΛNN and ΣNN systems at threshold. II. The effect of D waves
H. Garcilazo, A. Valcarce, and T. Fernández-Caramés, Phys. Rev. C 76 (2007)
Three-body hypernuclei in pionless effective field theory
F. Hildenbrand and H.-W. Hamme, Phys. Rev. C 100, 034002 (2019)
Investigation of the nnΛ bound state in pionless effective theory
Shung-Ichi Ando, Udit Raha, and Yongseok Oh, Phys. Rev. C 92, 024325 (2015)
Strange tribaryons
T. Fernández-Caramés, A. Valcarce, H. Garcilazo, and P. González, Phys. Rev. C 73, 034004 (2006)
KEK-PS E471実験による の発見によって行われた理論的な研究。 constituent quark cluster model を用いてバリオン数3、ストレンジネス数-1の tribaryon の存在を理論的に調べた。本研究ではは束縛しなかったが、内二つのチャンネル(I, J) = (1, 1/2) , (0, 1/2)は引力であり、三体閾値のわずか上であった。
Three-body structure of the nnΛ system with ΛN−ΣN coupling
E. Hiyama, S. Ohnishi, B. F. Gibson, and Th. A. Rijken, Phys. Rev. C 89, 061302 (2014)
束縛状態を coupling を取りいれて計算した。計算方法はGauss expansion method を用いた variational method。使用したポテンシャルはNSC97f YN potential とAV8 NN potential。これらは を再現したが、 は束縛しなかった。逆にどのポテンシャルを変えれば を再現できるのかを調べた。すると、YN NSC 97 potential ( coupling)を1.2倍、あるいはnn potential を1.35倍すれば は弱い束縛をすることが分かった。( coupling は束縛を強くする。)しかし、この場合は、 が over binding してしまう。 つまり、GSIの結果を説明するようなパラメータは見つけることが出来なかった。
A Λnn three-body resonance
H. Kamada, K. Miyagawa and M. Yamaguchi, EPJ Web Conf., 113 (2016) 07004
系 () のファデーエフ方程式をcomplex energy methodを用いて解いた。束縛状態はなかったが、共鳴状態は見つかった。NN, YN Nijmegen potential を用いた結果は で会った。preliminary のNijmegen YN potential (NSC97f)を用いると、 となった。
この論文では、YN Nijmegen potential (NijmYN89) と NN Nijmegen potential (Nijm93) を用いて共鳴・束縛を調べた。さらにYNとして最新のYN Nijmegen potential (NSC97f) も試した。結果は下図のようになった。元々のポテンシャルモデルでは束縛はせず、共鳴が存在することが分かった。 さらに として手でYN力を強くしていつ束縛状態が存在するのかを調べた。結果は1.2 倍程度であった。この結果もまたGSIの結果と矛盾する結果であるが、三体力、特にを仲介するものがうまく取り入れられていない可能性があるため、まだ束縛の可能性が完全に排除されたわけではない。

Properties of the bound Λ(Σ)NN system and hyperon-nucleon interactions
K. Miyagawa, H. Kamada, W. Glöckle, and V. Stoks, Phys. Rev. C 51, 2905 (1995)
Dibaryon
On the history of dibaryons and their final observation
H. Clement, Progress in Particle and Nuclear Physics, 93, 195-242 (2017)
Charge Symmetry Breaking
Observation of the Hypernucleus by the Reaction
S. N. Nakamura et al., Phys. Rev. Lett. 110, 012502 (2013)
INTRODUCTION Λ はパウリ効果を受けないため、任意の殻状態を取ることができる。Λ と核子の相互作用は弱いため、原子核中でも比較的長い寿命 を持ち、その結果ハイパー核準位の幅は数 100 keV と細い。
これまで行われてきた 、() 反応では、中性子標的が存在しないため素過程を用いた運動量キャリブレーションが出来ず、二次ビームの精度も限られているため分解能は 1.5 MeV 程度となっている。 本論文の () 反応では陽子を Λ に変換するため、素過程によって生成される Λ と Σ を用いた運動量キャリブレーションが出来る。さらに一次ビームの精度が良いため、sub - MeV オーダーの分解能を得ることが可能である。
本論文では 反応によって初めて観測された について報告する。 はエマルジョン実験によって観測されたという報告があるが、11 イベントにとどまっており、測定された質量も広がっており、基底状態だけではなく長寿命の isomeric states も含まれているとの指摘もある。 はA = 7, T = 1 のアイソスピン三重項 (, ) で測定されていない唯一のハイパー核である。これら三重項のコア核 は全て α 粒子の周りをハローである nn, pn, pp 対が囲んでいる原子核である。これらに Λ を追加した状態であるハイパー核でも同様に Λ は広がっており、Λ とハローの重なりも大きいと考えられる。さらに、これら三重項は 、A = 4 のアイソスピン二重項で確認されている Charge Symmetry Breaking (CSB) の測定にも重要である。
EXPERIMENT
Spectroscopy of the neutron-rich hypernucleus from electron scattering
T. Gogami et al., Phys. Rev. C 94, 021302 (2016)
Double Charge Exchange
Production of the Neutron-Rich Hypernucleus in the Double Charge-Exchange Reaction
P. K. Saha et al., Phys. Rev. Lett. 94, 052502 (2005)
INTRODUCTION Double Charge Exchange (DCX) による反応は断面積が小さいため測定が難しい。過去には、FINUDA による () 反応が測定されたが、 崩壊による Background が大きく上限を決めるにとどまっている。
DCXには二種類の過程、二段階過程と一段階過程があると考えられる。二段階過程では下図のように荷電交換とΛ生成がそれぞれ起こる。一段階過程では Doorway として が生成され mixing が起こることでDCXが起こる。
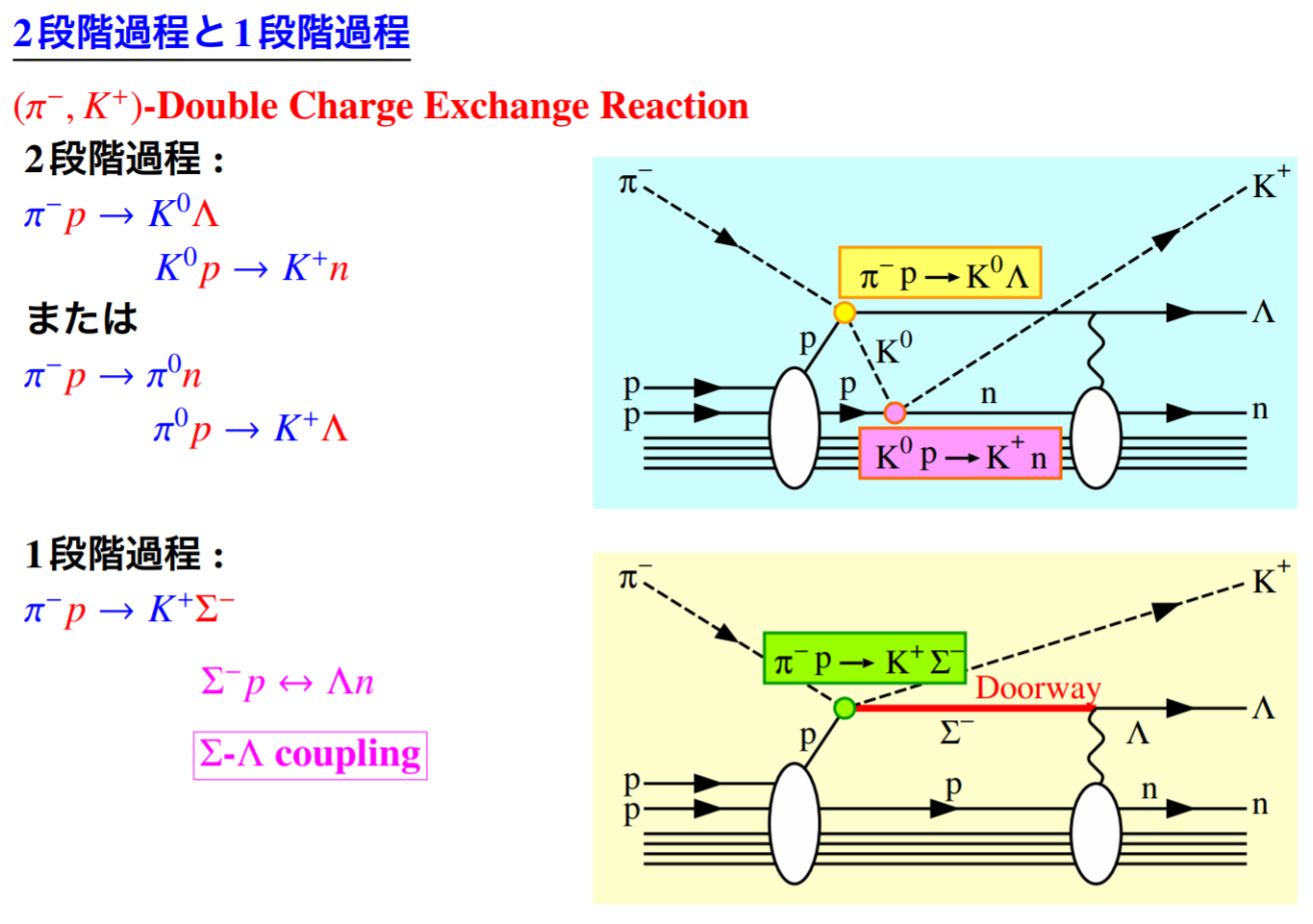
理論計算から、軽い ハイパー核では軌道角運動量が変化しない二段階過程の断面積が最も大きいとされている。これは中性子軌道が空いている標的を用いたときに起こり得る。ここから、 の生成断面積が大きいと考えられて おり、、 よりも大きいと考えられている ( 計算値はそれぞれ 70.0 nb/sr, 8.6 nb/sr, 0.5 nb/sr )。標的である は中性子が 5個、は 6 個、は 8 個。入射の運動量は1.05 GeV/c が最適と考えられており、これは 反応の時と同じである。一方、一段階過程の断面積は の混ざり度合に依存し、例えば で と計算されている。実験によりこの情報を抜き出すことが期待される。
本実験の目的は、まず DCX を成功させることであり、最も断面積が大きいとされる 生成を行った。ここから、さらなる中性子過剰ハイパー核 などの生成メカニズムなどを調べることが期待される。
Experiment 実験は KEK-PS の12 GeV 陽子ビームを用いた (KEK-PS-E521実験) 。用いたスペクトロメータはSKS。標的の厚さは 。
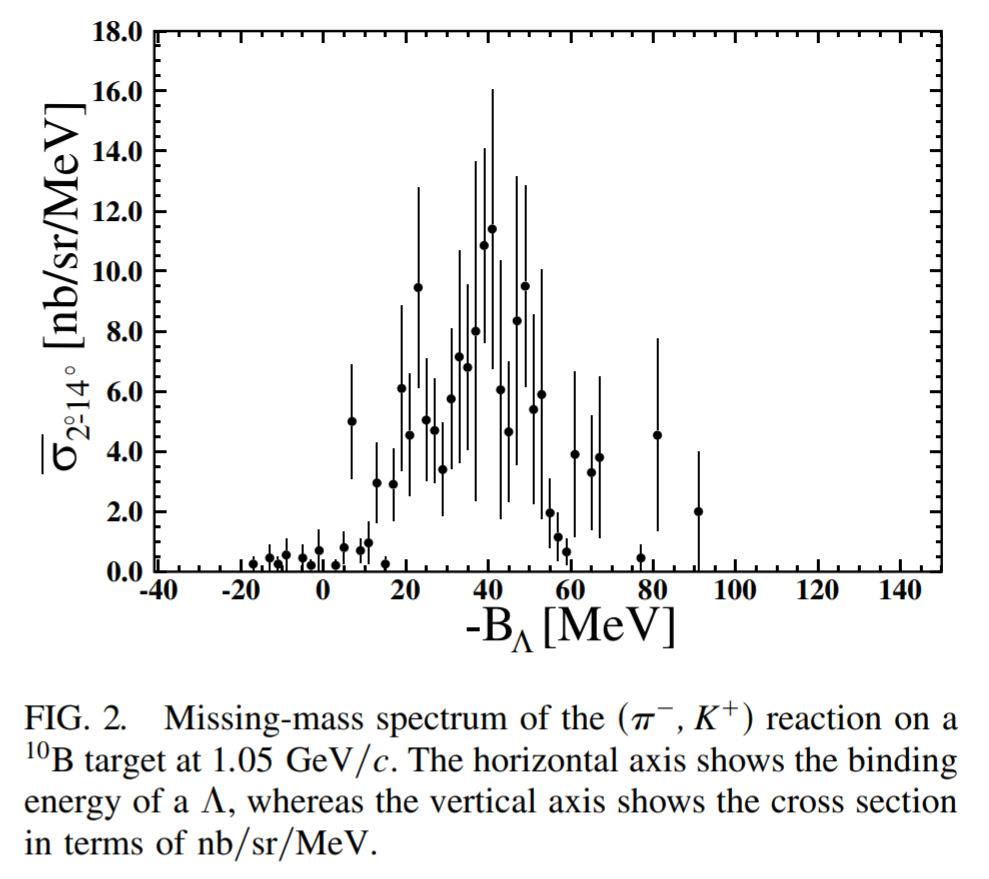
まず、断面積が大きいと考えられている で実験を行った。この状態での Missing Mass 分布が Fig.2 であり、縦軸は実験室系での を平均したものを示している。入射 は 個であり、束縛領域のイベントは 7 個、QF イベントは 138 個であった。仮に束縛が全て だとしても断面積は である。これは基底状態の doublet が二段階過程で生成されると仮定して計算された よりもかなり小さい。
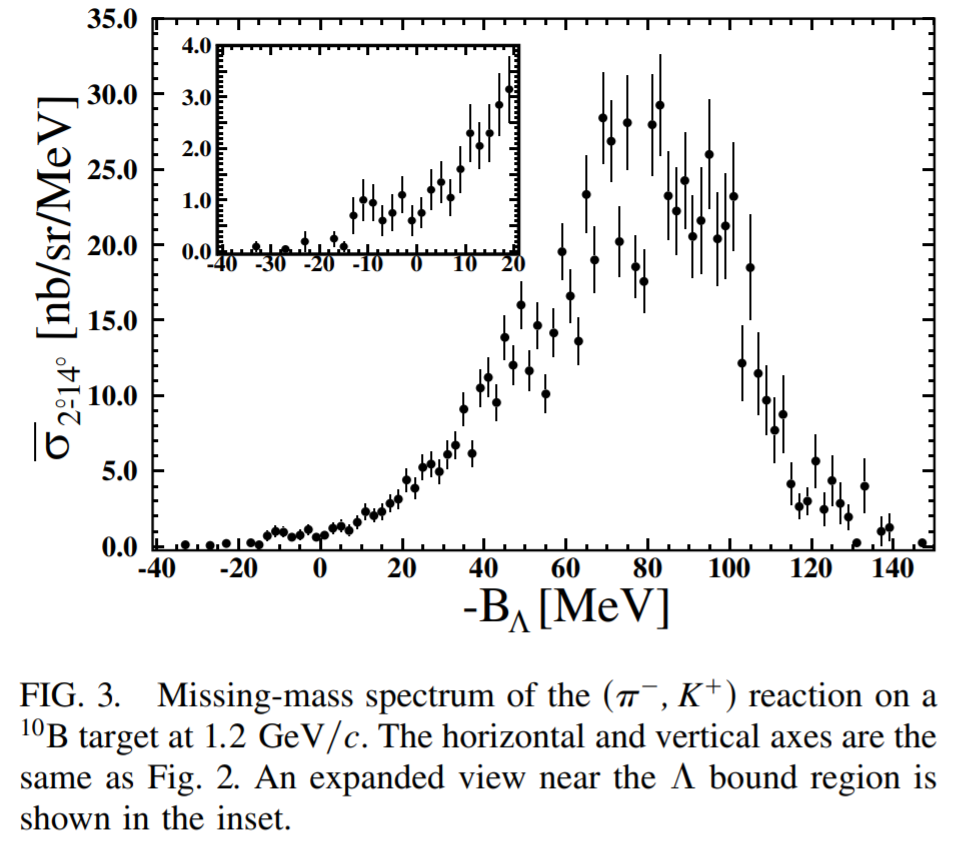
次に channel が開く、入射 で行った。ここでは が Doorway となる一段階過程も寄与していると考えられる。この運動量では 個の を照射した。束縛領域のイベントは 47個、QF イベントは 3064 個であった。
この実験のキャリブレーションのために 標的に対して 反応を測定した。この基底状態を参考にして、本実験の preciion = 0.23 MeV、resolution = 2.5 MeV (FWHM) と見積もった。
DISCUSSION 図からわかるように、ピークは確認できなかったが、束縛領域に有意なシグナルがある。 の領域を全てシグナルと考えると、 の生成断面積は となる。一方で、 から Back Ground を見積もると であり、 Back Ground を差し引いた後の断面積は となる。本実験は分解能が 2.5 MeV と良く、 のデータを参考にしても Quasi Free のもれ込みは少ないと考えられるが、仮に Quasi Free を線形で束縛領域まで外挿して差し引くと、 の生成断面積の下限は となる。
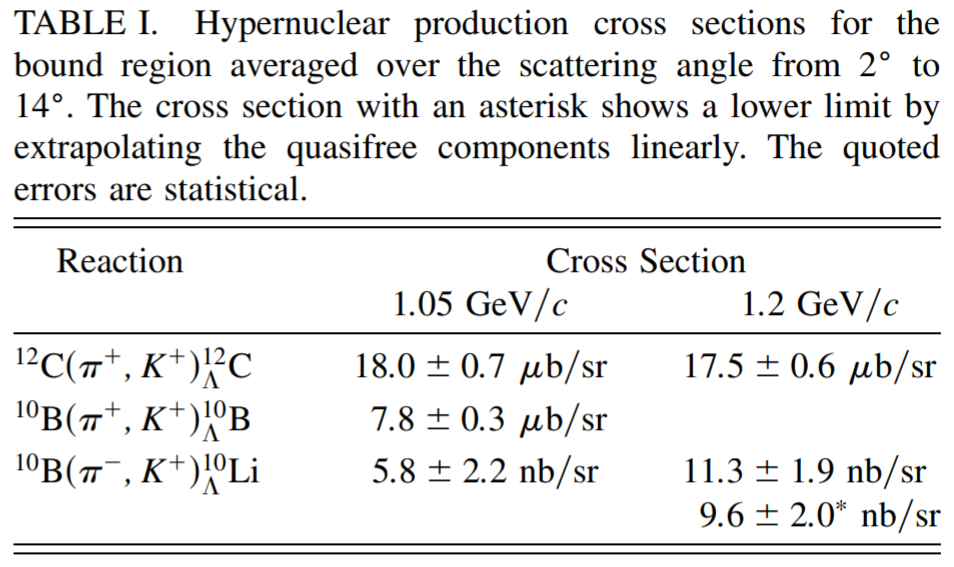
以上の結果を踏まえて導出した生成断面積が下表である。これは、二段階過程を踏まえて理論計算された 、 よりも非常に小さく、運動量依存性も反対である。ここから、 を経由する一段階過程が重要になってくると期待される。
Missing-mass spectroscopy with the reaction to search for
R. Honda et al., Phys. Rev. C 96, 014005 (2017)
Repulsion and absorption of the Σ-nucleus potential for Σ−−5He in the 6Li(π−,K+) reaction
Toru Harada, Ryotaro Honda, and Yoshiharu Hirabayashi, Phys. Rev. C 97, 024601 (2018)
Search for hypernucleus by the reaction at
H. Sugimura et al., Phys. Lett. B, 729, 39-44 (2014)
Evidence for Heavy Hyperhydrogen
M. Agnello et al., Phys. Rev. Lett. 108, 042501 (2012)
First observation of the hyper superheavy hydrogen
M. Agnello et al., Nuclear Physics A, 881, 269-287 (2012)
Hypernuclei
Evidence for a bound state of the Σ4 He hypernucleus
R.S. Hayano et al, Phys. Lett. B, Volume 231, Issue4, 16 November 1989 Pages355-358
Observation of a 4ΣHe Bound State in the 4He(K−,π−) Reaction at 600MeV/c
T. Nagae et al., Phys. Rev. Lett. 80, 1605 (1998)
Coulomb-assisted Σ−-nucleus bound states in the (K−,π+) reaction
Toru Harada, Yoshiharu Hirabayashi, Nucl. Phys. A 829, 1-2, 1 (2009) 100-125
S = -2 physics
Possible Lightest Hypernucleus with Modern N Interaction
Kaonic Nuclei
N = 3 system
Discovery of a strange tribaryon S0(3115) in 4He(stopped K−,p) reaction
T. Suzuki et al, Phys. Lett. B 16 263-269 (2004)
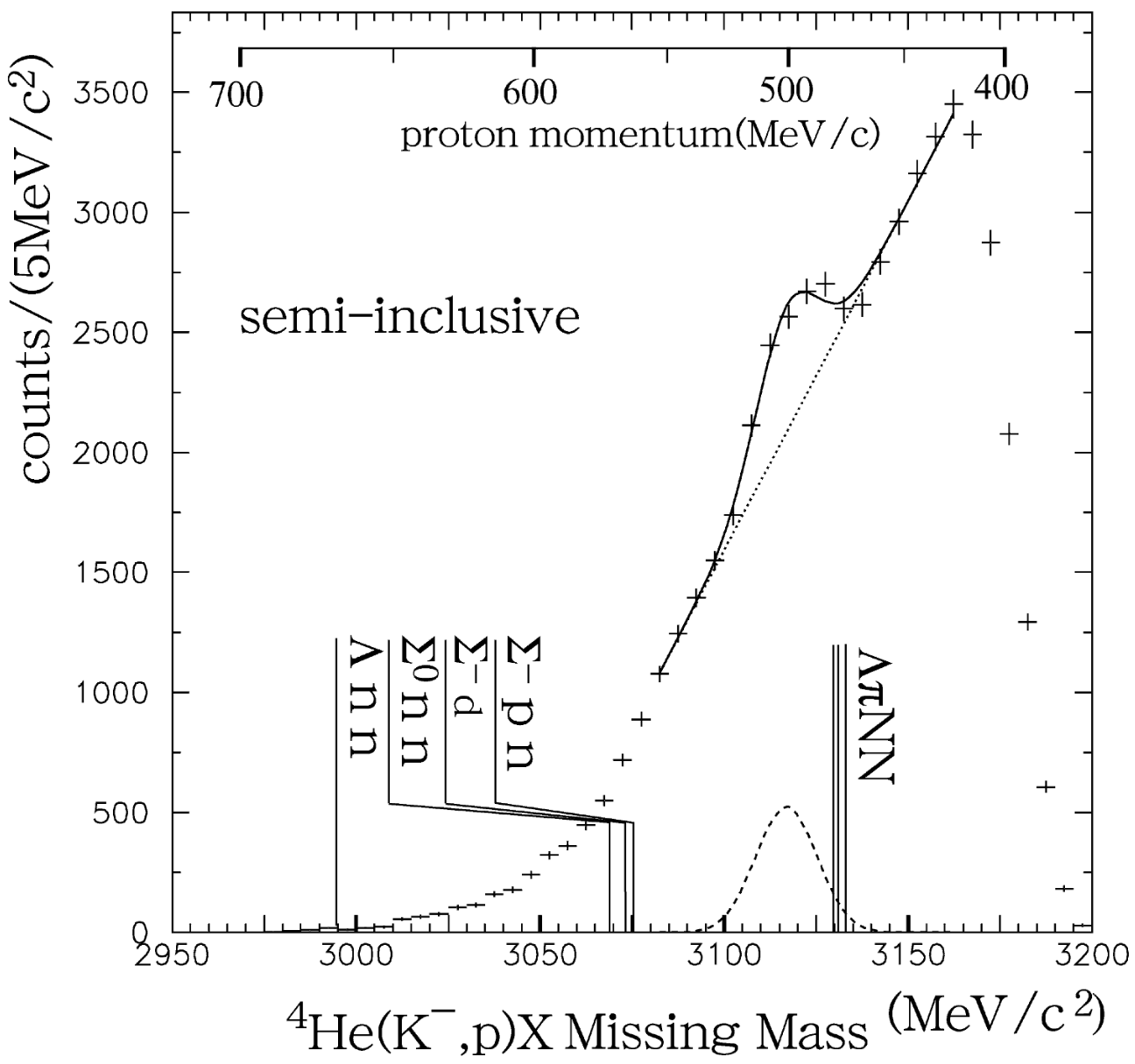
KEK-PS E471 実験。元々反応を用いて の deeply bound state を探そうととしていた。[ + n ]。アイソスピンが0である状態は明石・山﨑によって予言されていた。 試しに + p を探して見たところ、有意なピーク構造が観測された。これは元来予言されていなかったものである。
下図は測定結果である。図からみれるように3115 MeV付近に有意なピーク構造が確認できる。有意度は13 σ。幅は信頼区間 95 %で21 MeV 以下。質量からと名付けた。の下に四つの主なdecay modeが考えられる。崩壊におけるQ値を計算すると、は120 MeV、 は50 MeV程度である。の場合、Q値が大きいために の p が実験の検出器に届く筈である。実際には届いていないことから主な decay mode は であると考えられる。また、 stopped あたり が出来る割合は約 1 % である。
得られた は電荷0、ストレンジネス-1、バリオン数3、アイソスピン1である。幅が狭いため、Λハイパー核やΣハイパー核の励起状態としては考えにくい。様々な理論予想とは質量がかなり乖離しており、より詳細な研究が必要である。
Indication of a strange tribaryon S^+ from the ^4He(stopped K^-,n) reaction
M. Iwasaki et al., arXiv:nucl-ex/0310018 (2004)
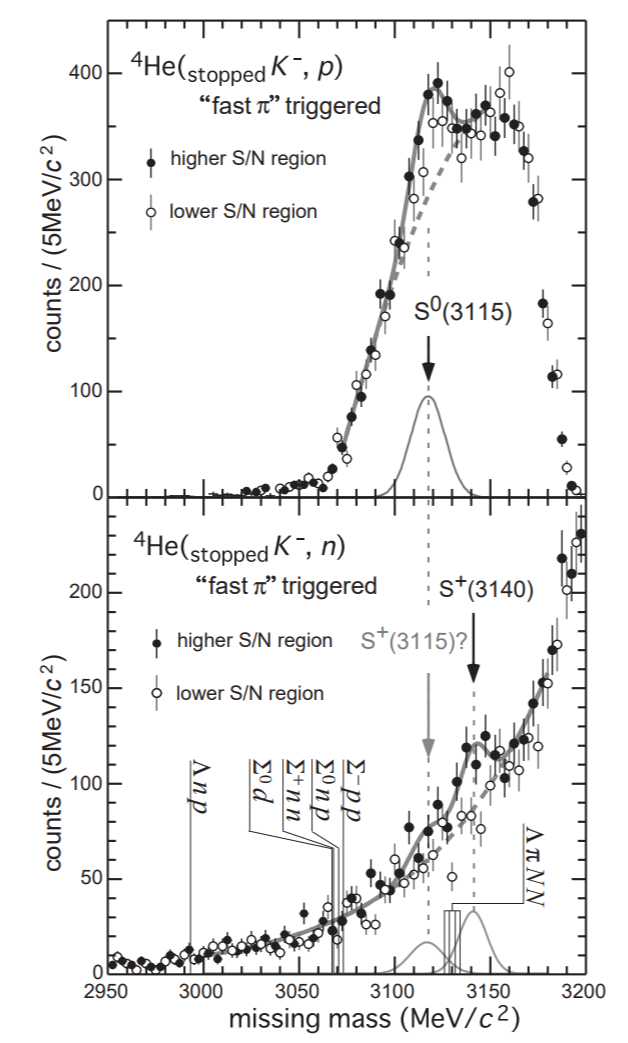
KEK-PS E471実験。arXivにしか出ていない? 上述の論文によって、 の発見が報告された。これはT = 1 、Z = 0である。それでは T = 0の状態はあるのか?明石・山﨑によって予想された状態はT = 0, Z = 1, M = 3194 MeVの状態である。これはで見つけることが出来るはずである。ただし、この反応では T = 0とT = 1 の二つの状態がSとして生成される。
下図が実験結果。上は前回の実験でも得られたである。下がneutronで見たスペクトルである。バックグラウンドを差し引くと、二つのピークがあるように見える。3115付近に見えるものは有意度としてはい低いが、 と同じ質量領域に存在することからこれは I = 1 のアイソスピンパートナーであると考えることが自然である。一方で、3140付近に見えるものの有意度は3.7 σである。3115とは違う領域に存在するため、これは I = 0 の状態と考えるのが自然である。
Search for strange tribaryon states in the inclusive 4He(Kstopped−,p) reaction
M. Sato et al., Phys. Lett. B 659, 107-112 (2008)
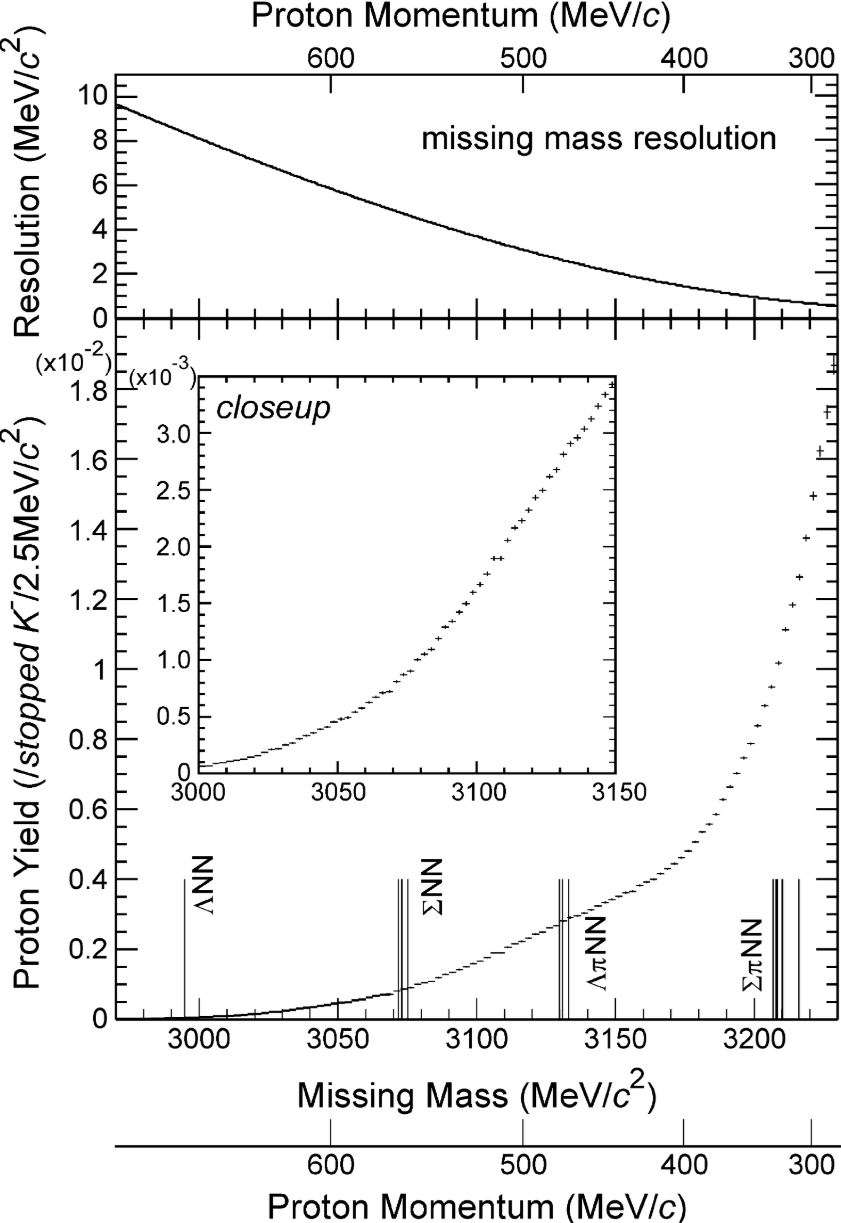
KEK-PS E549実験。上記のように) の発見がE471実験により主張された。E471実験の後、FINUDAが 反応において p スペクトルにピーク構造を発見した。しかし、彼らはこれは新粒子ではなく "quasi" deuteron のよる の捕獲によるもの () であるとし、 も同じ理由によるものであると結論した。一方でこれに対する反論もさらに挙がっており、さらなる実験が求められている。本論文は同じ粒子を同じ反応[ + p ] によって探索したものである。ただし、分解能、統計ともに上がっている。
実験結果が下図である。今回の測定では有意なピーク構造は観測されなかった。stopped あたりこの状態が作られる分岐比の上限は、 (Γ = 0 MeV)、 (Γ = 20 MeV)、 (Γ = 40 MeV) と決定された。この結論は、前回実験の が約 1 %であるという結論を否定する結果である。(佐田さんのD論では「E471実験のピーク構造は検出器キャリブレーション不足によるものである」と書かれている)
Search for strange tribaryons in the He4(Kstop−,nπ±) reaction
H. Yim et al., Phys. Lett. B 688 43-49 (2010)
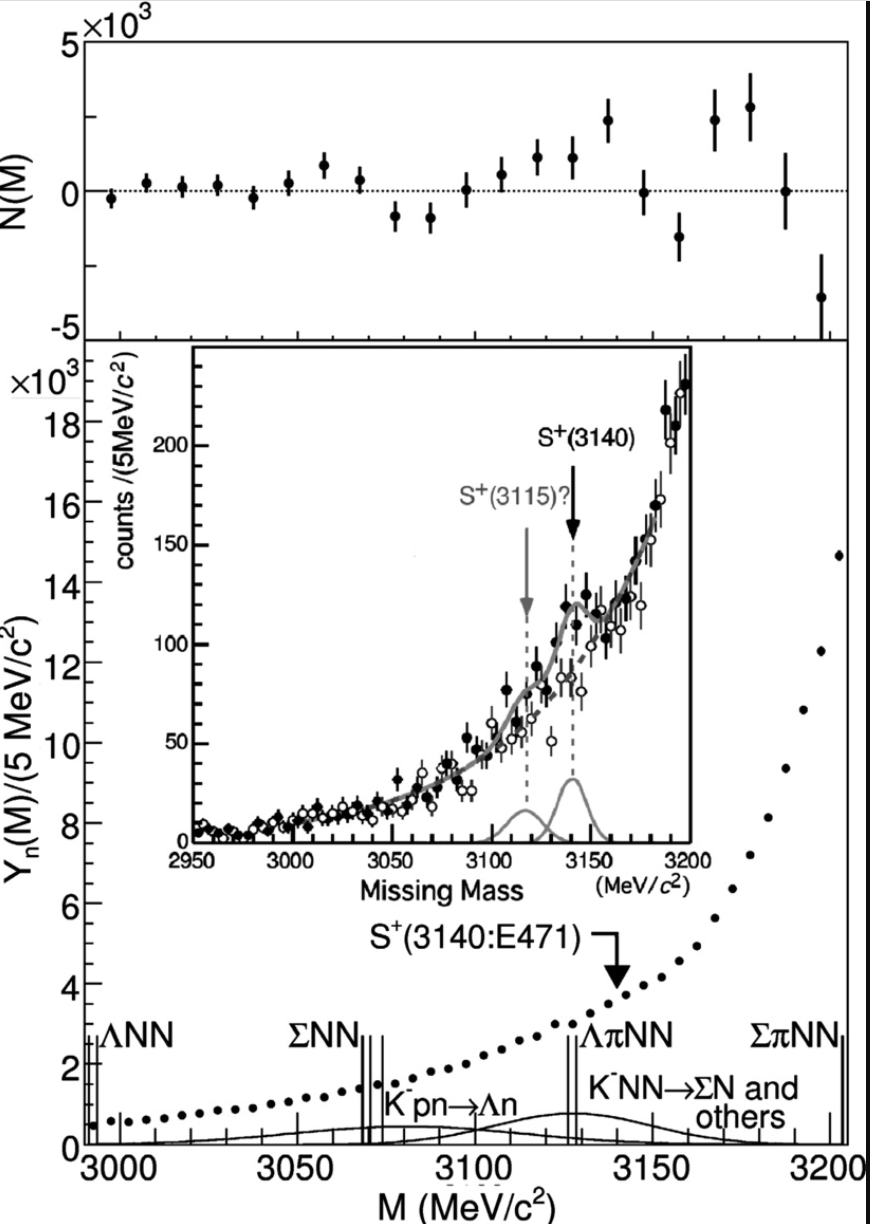
KEK-PS E579実験。E471実験で発見されたを確かめるために行った。今回は前回のように中性子を捉えるだけではなく、Sの崩壊によって生じるであろうも同時に取得した。前回実験と比べて、統計は6倍、分解能は1.5倍であり、バックグラウンドも大幅に削減した。
結果は下図。今回は有意なピーク構造は確認されず、上限を定めた。
Strange tribaryons as K¯-mediated dense nuclear systems
Y. Akaishi, A. Dote and T. Yamazaki, Phys. Lett. B 613 140-147 (2005)
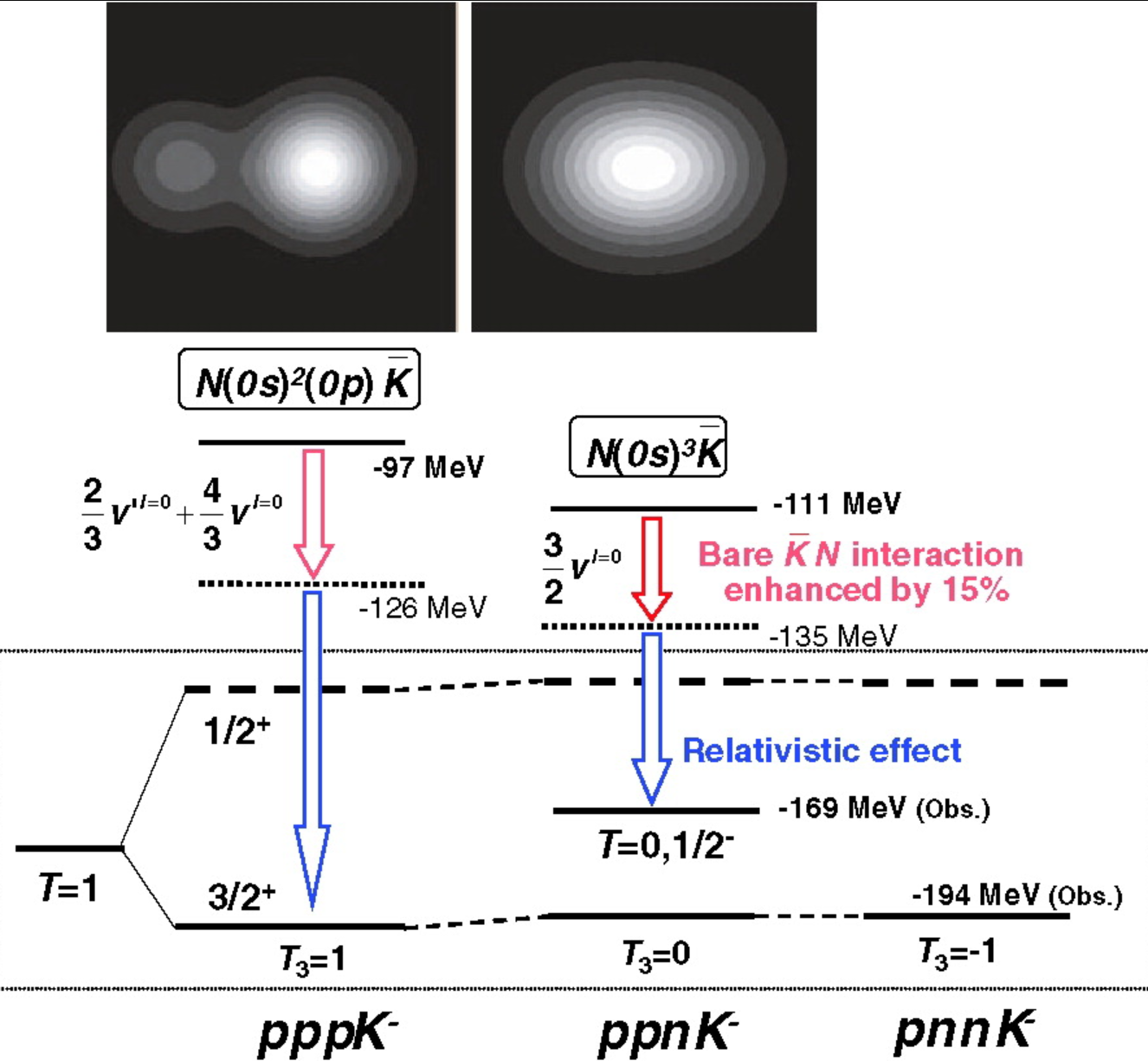
KEK-PS E471実験は元来、明石・山﨑による の深い束縛状態の予想により行われたものである。この理論予想は、I = 0 が基底状態 m = 3195 MeVである、I = 1 はそれより 87 MeV上に存在する励起状態であった。しかし、E471実験の結果は I = 1 が3115 MeVに基底状態として存在するというものであった。これはpnnKの閾値からも低い状態である。さらに見つかったもまた、である。元々の理論予想はそれぞれ、 97 MeV と 118 MeVであり、想定以上に深く、 I の順番が入れ替わっているというのは非常に興味深い。本論文ではこの解決について議論する。
まず、状態について議論する。I = 0 の相互作用は非常に強い引力であると考えられており、この状態の数が全体の束縛エネルギーに大きく寄与していると考えられる。 T = 0 の(NNNK)について考える。これは T = 1/2 のコア原子核にKが結合したものである。この時、 である。一方で、 T = 1 の状態で最もあり得るのは、次の二つの線形結合である。、 この中で、一つ目の組み合わせは I = 0 の結合の数が多い。したがって、の強さによっては I = 1 の方が基底状態になり得る。ただし、この項は N が一つ 状態に入らなければならないので、このコアの励起エネルギーとの競合である。下図はこれらを視覚的に表した図である。
論文の以下では、さらに相対論的効果、原子核が縮んだうえでのls力の変化を考慮している。ls引力は原子核が小さい方が強いため、計算値は実験により近づく。さらに 相互作用が原子核中で強くなると仮定すればこの実験値はある程度再現できる。
Exotic Hadron
Observation of a Resonant Structure in
M. Abilkim et al., Phys. Rev. Lett. 124, 112001 (2020)
について
Determination of the Lightest Strange Resonance or , from a Dispersive Data Analysis
J.R. Pelaez and A. Rodas, Phys. Rev. Lett. 124, 172001 (2020)
Momentum dependence of the imaginary part of the - and - nucleus optical potential
The CBELSA/TAPS Collaboration, The European Physical Journal A 62, 297 (2016)
Neutron-rich Nuclei
Evidence for the First Excited State of
A. A. Bezbakh et al., Phys. Rev. Lett. 124, 022502 (2020)
Nuclear Structure
Comparing proton momentum distributuions in A=2 and 3 nuclei via and measurements
Jefferson Lab Hall A Tritium Collaboration, Phys. Lett. B 797, 134890 (2019)
Simulation Technique
FSI and Quasi Free
David Gaskell D thethis
Benjamin Clasie D thethis
Including Fermi Motion
Medium effects on Ξ− production in the nuclear (K−,K+) reaction
Toru Harada and Yoshiharu Hirabayashi, Phys. Rev. C 102, 024618 – Published 17 August 2020
Optimal approximation to elastic and inelastic scattering on a bound nucleon system
S. A. Gurvitz, Phys. Rev. C 33, 422 – Published 1 February 1986
Statistics
Statistical Analysis in experimental particle physics
Goodness of fit tests for weighted histograms
N.D. Gagunashvili, Nucl. Inst. A, Volume 596, Issue 3, 11 2008, Pages 439-445
Others
Quantum Measurements of Time
Lorenzo Maccone and Krzysztof Sacha, Phys. Rev. Lett. 124, 110402 (2020)
量子力学(倉澤さん)
散乱の章が面白そう
A General Expression for Symmetry Factors of Feynman Diagrams
Isobaric Analogue States
C.D. Palmer and M. E. Carrington
Feynman DiagramのSymmetry Factorの計算方法
ctrl4 --> ctrl+K ctrl6