

Next: 単位系と次元
Up: No Title
Previous: No Title
まずこれまで良く勉強したはずの重力と電磁力を考えよう。MKS単位系で重力と
電磁力は
で与えられる。
陽子は重さMp、荷電は電子素量eを持つわけであるから、各々
となる。従ってG MpMp と
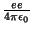 (単位は[kg・m3/sec2])
が2つの場合で比べるべき量である。更に踏み込むと、今後出てくる弱い力
や強い力が 1/r2の依存性を持っているという保証はないし(実際に
も1/r2に従わない)どんな未知の量が現れるやも知れぬ。
従ってここで比べるべき量を無次元化しておき、ある距離
での力を比較することにすると便利であろう。このように無次元化した
量を結合定数(カップリングコンスタント)と呼ぶ。
(単位は[kg・m3/sec2])
が2つの場合で比べるべき量である。更に踏み込むと、今後出てくる弱い力
や強い力が 1/r2の依存性を持っているという保証はないし(実際に
も1/r2に従わない)どんな未知の量が現れるやも知れぬ。
従ってここで比べるべき量を無次元化しておき、ある距離
での力を比較することにすると便利であろう。このように無次元化した
量を結合定数(カップリングコンスタント)と呼ぶ。
[kg・m3/sec2]は[J・m]の単位なので、これに対応する物理定数を
探してみるとプランク定数h[J・s]と光速c[m s-1]の積がこれにあたる。
実際にはプランク定数を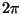 で割った
で割った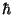 を用いて無次元化する習慣が
ある。結合定数は一般に
を用いて無次元化する習慣が
ある。結合定数は一般に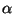 という変数を使うので
という変数を使うので
である(但し
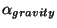 という標識は一般に使われるものではない)。
実際の値を入れてみると
という標識は一般に使われるものではない)。
実際の値を入れてみると
となる。
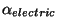 は通常
は通常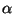 とかかれ微細構造定数
(fine structure constant)と呼ばれる(歴史的な理由)。
このように無次元化しておくと単位の取り方によらず普遍的に力の
強さを比べることが出来るわけである。
以上の考察から陽子間に働く重力は電気力に比べ1036倍も弱いことがわkる。
とかかれ微細構造定数
(fine structure constant)と呼ばれる(歴史的な理由)。
このように無次元化しておくと単位の取り方によらず普遍的に力の
強さを比べることが出来るわけである。
以上の考察から陽子間に働く重力は電気力に比べ1036倍も弱いことがわkる。
さて準備(復習)は完了?


Next: 単位系と次元
Up: No Title
Previous: No Title
2000-02-04
![]() で割った
で割った![]() を用いて無次元化する習慣が
ある。結合定数は一般に
を用いて無次元化する習慣が
ある。結合定数は一般に![]() という変数を使うので
という変数を使うので