

Next: 重力定数 Gの測定
Up: No Title
Previous: はじめに(重力と電磁力の復習)
ここで単位系に関して整理しておく。MKS単位系から自然単位系へ頭を
切り替えていただく。
自然界には基本的な3つの次元(時間、長さ、質量)があって、すべての物理量は
これの組合わせになる。この各々の次元を記述するのが単位系である。
これは便宜的なものであるから、独立な次元をもった自然定数を3つ
とりだし、それを基本とした単位系があってもよい。
特殊相対論により時間と空間が同等なものとして認識され光速度不変の原理が
生まれた。すなわち
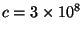 [m/s]である。量子力学の不確定性関係は
運動量と長さ、又は時間とエネルギーを結び付けプランク定数hが生まれた。
よく使われるのはhを
[m/s]である。量子力学の不確定性関係は
運動量と長さ、又は時間とエネルギーを結び付けプランク定数hが生まれた。
よく使われるのはhを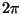 で割った
で割った
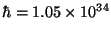 [J・s]である。
[J・s]である。
もうひとつは重力定数であるべきであろうが、こいつは前述のように小さすぎて
使いにくい。また、例えば質量の次元[kg]を自然定数の次元で書くと
[
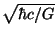 ]となってこれまた使いにくい。よって質量の次元は
便宜的に使いやすいものを導入することになっている。これをMとすると
]となってこれまた使いにくい。よって質量の次元は
便宜的に使いやすいものを導入することになっている。これをMとすると
[質量]=[
M]、[長さ]=[
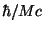
]、[時間]=[
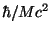
]
[エネルギー]=[Mc2]、[運動量]=[Mc]
である。質量のかわりにそれと等価なエネルギーEを基本単位として使うと、
[質量]=[
E/
c2]、[長さ]=[
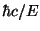
]、[時間]=[
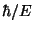
]、
[エネルギー]=[
E]、[運動量]=[
E/
c]
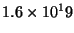 J
に相当する)。
実際の粒子の質量はMeV[106eV]からGeV[109eV]の量なのでMeV
を基本単位だと思い直して書き直すと、
J
に相当する)。
実際の粒子の質量はMeV[106eV]からGeV[109eV]の量なのでMeV
を基本単位だと思い直して書き直すと、
[質量]=[MeV/
c2]、[長さ]=[
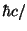
MeV]、[時間]=[
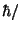
MeV]、
[エネルギー]=[MeV]、[運動量]=[MeV/
c]
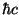 の値をMeVを用いて書き直す
と便利である。
の値をMeVを用いて書き直す
と便利である。
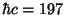 [MeV fm]でfmは10ー9mである。
(実際200 MeV・fmと覚えておけば十分)。
fmは素粒子の大きさのスケールなのでこれもまた便利に使われる。
[MeV fm]でfmは10ー9mである。
(実際200 MeV・fmと覚えておけば十分)。
fmは素粒子の大きさのスケールなのでこれもまた便利に使われる。
[質量]=[MeV/c2]、[長さ]=[fm]、[時間]=[fm/c]、
[エネルギー]=[MeV]、[運動量]=[MeV/c]。
自然単位系は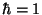 、c=1とおいてしまうものである。すると、
、c=1とおいてしまうものである。すると、
[質量]=[MeV]、[長さ]=[1/MeV]、[時間]=[1/MeV]、
[エネルギー]=[MeV]、[運動量]=[MeV]
であり、自然単位系で書かれる式はすべてエネルギーの単位に統一できてしまう。
これでおしまいといいたいところだが、別の単位系に換算したいときはかならず
ある。結局、自然単位系で計算し値をもとめたら
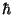 とcをかけて適当な単位にしてしまえば良いわけである。
そのときに使う換算式が
とcをかけて適当な単位にしてしまえば良いわけである。
そのときに使う換算式が
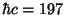 [MeV fm]となる。例えば速度は
無次元量で換算にはcをかければよい。
[MeV fm]となる。例えば速度は
無次元量で換算にはcをかければよい。
以下未完


Next: 重力定数 Gの測定
Up: No Title
Previous: はじめに(重力と電磁力の復習)
2000-02-04
![]() [m/s]である。量子力学の不確定性関係は
運動量と長さ、又は時間とエネルギーを結び付けプランク定数hが生まれた。
よく使われるのはhを
[m/s]である。量子力学の不確定性関係は
運動量と長さ、又は時間とエネルギーを結び付けプランク定数hが生まれた。
よく使われるのはhを![]() で割った
で割った
![]() [J・s]である。
[J・s]である。
![]() ]となってこれまた使いにくい。よって質量の次元は
便宜的に使いやすいものを導入することになっている。これをMとすると
]となってこれまた使いにくい。よって質量の次元は
便宜的に使いやすいものを導入することになっている。これをMとすると
![]() 、c=1とおいてしまうものである。すると、
、c=1とおいてしまうものである。すると、