重力定数 Gの測定

まずは小手試しにGを測定してみよう。とはいっても陽子同士の重力は 測定できそうにないので、もっとマクロな系で測ってみよう。 捻じればかりの測定も芸がないので別の方法をもちいる。

赤道軌道上に衛星放送のための静止衛生があるのはご存じだろう。 衛星放送と地上放送、おんなじ番組がやっているときに、両放送を 聞き比べたことがありますか？ なかったら是非聞いてみてください。 摩訶不思議な体験ができます。

#これって重力定数の決定に使えないかなー?

静止衛星に働く遠心力mv²/r(vは速度)が重力GmM/r²と釣り合う 条件よりv²=GM/rであり、静止条件は 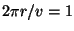$2\pi r/v=1$日=86400secなので

$$GM={\frac{2\pi}{86400}}^2 r^3$$

である。従って静止衛星までの距離を測定すればGMが求まることになる。 ここで、地上放送を静止衛星に送り帰ってくるまでの時間を2Tとすると r=2CTであるので、2Tを求めればよい。 地上放送のフーリエ成分を sin(w(t-T))とすると衛星放送は sin(w(t+T))になるはずで、この二つの音声を混ぜると

$$\sin(wt-wT)+\sin(wt+wT)=2\cos(wt)cos(wT)$$

である。これは所謂エコーである。すなわちもとの音声スペクトラムが 「白(すべての周波数が均一に現れる」ならば周波数 パワースペクトラムは 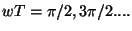$wT=\pi/2,3\pi/2....$のときゼロとなる周期関数になる(ある周波数の音が聞こえない)。 実際の音声は定常的でないので場合によっては(Tの大きさ)山びこのように 聞こえるかも知れない。

以下未完 実際の値 <-

$$\6.667 \times 10^{-11}, M=5.98\times 10^{24}[kg],T=0.1408[sec]$$

->