


Next: [問題 2-4]これはなんでしょう
Up: パーツ屋に行ってみよう
Previous: [問題 2-3]これはなんでしょう。
答え:コイル(トランス)
コイルはインダクタンスとよばれ電子回路では一番やっかいなものです。
電磁気でならったようにコイルとは電流の変化を嫌うダンパーみたいなもので、
磁力線を利用しているため自己インダクタンスだけでなく相互インダクタンスも
もちます。自己インダクタンスを利用するものをコイル、相互インダクタンスを
利用するものをトランスとよびます.
インダクタンスの電子回路での利用はほとんど高周波共振回路と電源回路に
かぎられます。形状は千差万別ですが、電源トランスだけは重いのですぐ分かります。
高周波用のコイルは抵抗と同じようなカラーコードで表されたものも多いです。
また例のセラミックコンデンサーと同じような104=
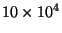 とかいう表示も
あります。
ただし単位はμHです。これは一見抵抗と区別がつきませんが全体が緑っぽいの
ものが多いようです。抵抗をテスターで測ってみるとゼロだったら嬉しいのですが
残念ながらコイルは長い導線なので数〜数10オームの抵抗をもちます。
一般に高周波コイルやトランスの規格は外見からは分からないことの方が多いです。
ラジオの中を覗くと高周波用トランスや微調用可変コイルがいっぱい入っています
ので一度中を見てみてください。
とかいう表示も
あります。
ただし単位はμHです。これは一見抵抗と区別がつきませんが全体が緑っぽいの
ものが多いようです。抵抗をテスターで測ってみるとゼロだったら嬉しいのですが
残念ながらコイルは長い導線なので数〜数10オームの抵抗をもちます。
一般に高周波コイルやトランスの規格は外見からは分からないことの方が多いです。
ラジオの中を覗くと高周波用トランスや微調用可変コイルがいっぱい入っています
ので一度中を見てみてください。
さてちょっと数式。電磁誘導の法則によると電圧と磁束の関係は
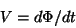 |
(7) |
です。
但し磁束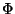 は 磁束密度B×断面積Sです。磁束は電流Iに
比例するので
は 磁束密度B×断面積Sです。磁束は電流Iに
比例するので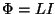 と書いてLを自己インダクタンスと定義します。
従って基本式は
と書いてLを自己インダクタンスと定義します。
従って基本式は
で与えられます。複素インピーダンスでいうならば前と同様に
 |
(9) |
です。
ここでちょっと磁束漏洩のない透磁率μの
トロイダル(ドーナッツ)に導線をn1回まいたコイルを考えてみましょう。
周長をlとすると磁束は一様で
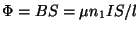 です。この磁束が
n回コイルを貫いていますから、回路全体としての起電力は
です。この磁束が
n回コイルを貫いていますから、回路全体としての起電力は
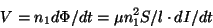 |
(10) |
従ってこのコイルの自己インダクタンスは
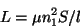 |
(11) |
で与えられ、自己インダクタンスは巻き数の二乗に比例する
ことが分かります。このトロイダル
に別の回線をn2回巻き付けると相互インダクタンスが発生しトランスとして
動作します。相互インダクタンスは;
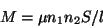 |
(12) |
となります。もうちょっと一般化して一次がわと二次側をサフィックスであらわすと;
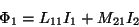 |
(13) |
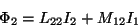 |
(14) |
時間微分すると
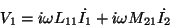 |
(15) |
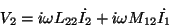 |
(16) |
一般に
M21=M12なので Mとおき直すと
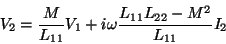 |
(17) |
となります。
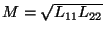 の時には周波数依存性が消える理想トランス
となり、ここで考えている場合はあきらかにこの条件を満たしています。
従って
の時には周波数依存性が消える理想トランス
となり、ここで考えている場合はあきらかにこの条件を満たしています。
従って
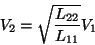 |
(18) |
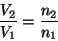 |
(19) |
同様にして、Mが大きな極限では
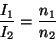 |
(20) |
となるので一次側と二次側のインピーダンス比は
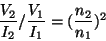 |
(21) |
になるわけです。 ちょっと式が多かったのですが、この問題は2000年度の
大学院入試問題になっていたので寄り道をしました。残念ながらできは
非常に悪かったと聞いています。



Next: [問題 2-4]これはなんでしょう
Up: パーツ屋に行ってみよう
Previous: [問題 2-3]これはなんでしょう。
2000-02-20


![]() とかいう表示も
あります。
ただし単位はμHです。これは一見抵抗と区別がつきませんが全体が緑っぽいの
ものが多いようです。抵抗をテスターで測ってみるとゼロだったら嬉しいのですが
残念ながらコイルは長い導線なので数〜数10オームの抵抗をもちます。
一般に高周波コイルやトランスの規格は外見からは分からないことの方が多いです。
ラジオの中を覗くと高周波用トランスや微調用可変コイルがいっぱい入っています
ので一度中を見てみてください。
とかいう表示も
あります。
ただし単位はμHです。これは一見抵抗と区別がつきませんが全体が緑っぽいの
ものが多いようです。抵抗をテスターで測ってみるとゼロだったら嬉しいのですが
残念ながらコイルは長い導線なので数〜数10オームの抵抗をもちます。
一般に高周波コイルやトランスの規格は外見からは分からないことの方が多いです。
ラジオの中を覗くと高周波用トランスや微調用可変コイルがいっぱい入っています
ので一度中を見てみてください。
![]() です。この磁束が
n回コイルを貫いていますから、回路全体としての起電力は
です。この磁束が
n回コイルを貫いていますから、回路全体としての起電力は