


Next: 簡単な応用:ラウドネススイッチの仕組みと基本的なフィルター回路
Up: 世の中のブラックボックスたち (交直流回路の概論をかねて)
Previous: 世の中のブラックボックスたち (交直流回路の概論をかねて)
さて、一般に負荷をつなぎたいから電源があるわけで、容易に想像できるように負荷
抵抗とコンデンサーの容量でリップル率がきまります。この時使うべきパーツの値を
などを簡単に決めるため
の処方箋が交流回路理論です。周期的なものを考えるときは実効値でかんがえ(フーリエ成分で
考える)、過渡的な応答を考えるときには微分方程式を解くか、ラプラス変換をするのが常套的
なやりかたです。まーラプラス変換をしなきゃならない時はほとんどないと思います。
では数式:RLCに対する瞬時値の応答は、
実効値の応答も複素インピーダンスで書けて、
です。これらは
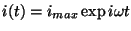 とおけば容易に確かめられます。複
素数は
位相の回り方をあらわしていています。普通電流を基準にして電圧の位相を考えま
す。
コイルの電圧の位相は90度進み、コンデンサーは90度遅れるということです。
実際に複素数の電流が流れてるわけではなく、これは一種の便法です。
とおけば容易に確かめられます。複
素数は
位相の回り方をあらわしていています。普通電流を基準にして電圧の位相を考えま
す。
コイルの電圧の位相は90度進み、コンデンサーは90度遅れるということです。
実際に複素数の電流が流れてるわけではなく、これは一種の便法です。
Figure:
RL直列回路
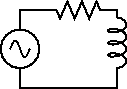 |
RとLを並べた回路に
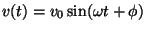 の起電力をかけた場合を考
えてみます。解くべき微分方程式は、
の起電力をかけた場合を考
えてみます。解くべき微分方程式は、
ですが、v(t).i(t) の変わりに複素数表示の
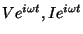 を
代入してみます。
このときV,Iは複素数で、例えば
を
代入してみます。
このときV,Iは複素数で、例えば
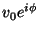 とおくと
とおくと
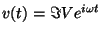 との関係を満たすことも簡単にわかります。ものの本ではこのとき
との関係を満たすことも簡単にわかります。ものの本ではこのとき
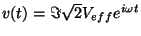 と書いてあることが多いです(複素数表示は一般に実効値で書くため)。ここではあ
まりこだわらないことにします。これは電灯線の電圧は141Vだと思い直すことに対応し
ます。さて
と書いてあることが多いです(複素数表示は一般に実効値で書くため)。ここではあ
まりこだわらないことにします。これは電灯線の電圧は141Vだと思い直すことに対応し
ます。さて
で、複素数表示(フェザー表示とも言う)が成り立つための条件が得られる。これと
複素共役な
もの、
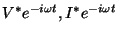 も微分方程式をみたすための条件は
も微分方程式をみたすための条件は
で、差をとってiをかければ、虚部がもとまり現実の世界に戻れます。すなわち
です。
従って、i(t)を得るためには複素表示で解いて虚部をみればよいことになります。
ポイントは:
- 微分・積分はそれぞれ
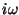 をかける
をかける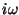 で割る操作
で割る操作
- 複素数表示でiをかけるのは
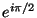 をかけることで90度位相を進めて
いることになる。
をかけることで90度位相を進めて
いることになる。
-
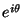 をかけることは
をかけることは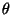 度位相を進めていることになる。
度位相を進めていることになる。
ということで、「信号がフーリエ分解でき、周波数を固定して考えて、後で重ね合わ
せればよい」という事実だけで、扱いがこんなにたやすくなるわけです。
Figure:
RLC直列回路
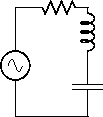 |
RLCを直列に並べるとインピーダンスZは
で、この絶対値が最小になるのは
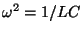 の時です。これを共振周波数と
いって
ラジオの同調回路や発信回路で重要な概念です。
の時です。これを共振周波数と
いって
ラジオの同調回路や発信回路で重要な概念です。



Next: 簡単な応用:ラウドネススイッチの仕組みと基本的なフィルター回路
Up: 世の中のブラックボックスたち (交直流回路の概論をかねて)
Previous: 世の中のブラックボックスたち (交直流回路の概論をかねて)
2000-02-20