乗算回路（pn接合の愉快な使い方)

これまで、トランジスタはシリコンで0.6Vでonになる理想的な増幅器として みてきましたが、立ち上がりはかなりnon-linearなものです。これを利用して 掛け算を実行する回路を作ることができます。 実際pn接合を流れる電流には;

$$I_D=I_S(\exp{eV_D/kT}-1) \, \, \,　e/kT=38.6/V @ 300^oK$$

という関係があります。ここでI_Sは飽和電流と言われ、GeはSiの10倍ほどあります。 これが実用領域での立ち上がり電圧の違いを生むわけです。ここをちゃんと見てみると ある動作点(あるベース電流の値)でのVーI曲線の傾きは

r_D=dV_D/dI_D

で与えられ、I_D=I₀ のとき

$$r_D = kT/e/I_0 = \frac{26}{I_0(mA)} \, \, \, (\Omega)$$

になります。これが内部エミッタ抵抗に見えることになります。

いま作動増幅回路の増幅率は外部コレクタ抵抗とエミッタ内部抵抗の比になること を使い、エミッタ内部抵抗に上のの式を使うと

$$A_V = R_c/r_e = \frac{eR_c}{kT} I_e$$

です。今エミッタ電流を例の低電流回路を外部電圧V₂で駆動してやると

$$V_O = R_c/r_e = \frac{eR_c}{kT} I_e \times V_1 \propto V1\times V_2$$

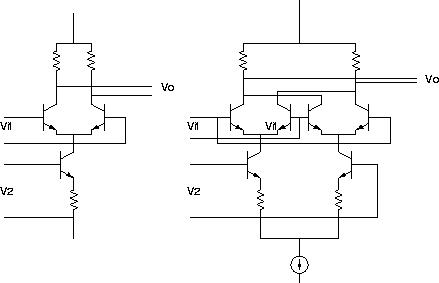
になります。図の左に示したものはもっとも簡単なものですが、V₂のバイアスの賭け方が難しいので、実際には右図のようなものを用います。 乗算のもっとも卑近な例が変調回路で、高度な電子回路によく使われる 手法です。

 

Figure: 掛け算回路の実際。基本(左)と高精度なもの(右