


Next: ミラー効果と増幅回路の周波数特性
Up: 負帰還と回路の周波数域特性(発振してこまるダメアンプとは)
Previous: 負帰還と回路の周波数域特性(発振してこまるダメアンプとは)
ちょっとRCで出来たローパスフィルターを考えます。出力は
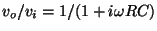 になります。
振幅と位相はそれぞれ
になります。
振幅と位相はそれぞれ
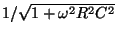 、
、
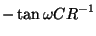 。
振幅をデシベル表示にすると
。
振幅をデシベル表示にすると
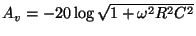 です。
この回路で低域から広域に行くとAv=0 [dB]から
です。
この回路で低域から広域に行くとAv=0 [dB]から
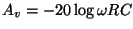 になります。
周波数が2倍になると(1オクターブ上がると)Avが6dB下がる(半分になる)わけです。
になります。
周波数が2倍になると(1オクターブ上がると)Avが6dB下がる(半分になる)わけです。
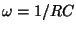 (時定数)の時、
(時定数)の時、
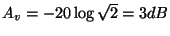 下がっているわけです。
従って周波数特性は普通ログログプロットされます。ここで、折れ線になって見えるわけです。
また位相は
下がっているわけです。
従って周波数特性は普通ログログプロットされます。ここで、折れ線になって見えるわけです。
また位相は
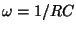 (時定数)のとき45度まわり、最終的には90度回ります。
2段異なった時定数を持ったRCフィルターがあるとAvはログログプロットで高周波領域
をみると2つの傾きをもったようになり
位相は最終的に180度回ってしまいます。
(時定数)のとき45度まわり、最終的には90度回ります。
2段異なった時定数を持ったRCフィルターがあるとAvはログログプロットで高周波領域
をみると2つの傾きをもったようになり
位相は最終的に180度回ってしまいます。



Next: ミラー効果と増幅回路の周波数特性
Up: 負帰還と回路の周波数域特性(発振してこまるダメアンプとは)
Previous: 負帰還と回路の周波数域特性(発振してこまるダメアンプとは)
2000-02-20