 |
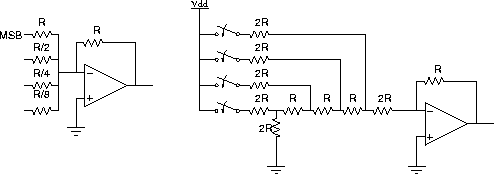
もっとも基本的なDA変換は足し算回路でつくります。オペアンプ の回路で示した足し算回路の帰還抵抗をRとし 変換したいデジタル数値の最大ビット数に対応するスイッチ をR/1、次のビットをR/2 最少ビットをR/2nの抵抗で足し算します。これでオーケーです。 この回路は簡単ですが10ビットもあるようなDA変換では最大 抵抗値と最少抵抗値の比は1024分の1にもなります。普通の抵抗の 精度が0.5%ですから、実用化はほとんど不可能になります。 また抵抗の温度変化にも大変弱い回路です。
この欠点を克服したのが、Rー2R梯子型DA変換で、とっても標準的なものです。 図にしめしたものは4ビットですが、いくらでも拡張可能です。 図ではちゃんとかかれていませんがONのビットは電源に、OFFのビットは 接地されるようにスイッチは動くと思ってください。
オペアンプから近い側からみてはじめの節から入力を見るとMSBのスイッチが 接地されていると2R//2RでRの抵抗と等価です。以下同様に各段を過ぎて LSBからみた抵抗値はやっぱり2Rで、LSBをONにすると、 結局最後の節はVdd/3の電圧になります。この電圧による最初の節の電圧は 1/8です。中間の段でも同様です。結局入力電圧はそれぞれの1/8, 1/4,1/2,1/1が足されたことになり(テブナンの定理)でみごとにDA変換が 成り立っています。この回路はRの抵抗値に対する誤差が伝搬しにくいのが 特徴です。同じような抵抗値は精度良く作りやすいいのもポイントですね。