


Next: 演算・記憶・インターフェイス
Up: デジタル回路との入出力
Previous: サンプル&ホールド回路とサンプリング定理
さて8倍オーバーサンプリングをやってしまうと、内部の情報は
擬似的に8×22.05kHzまで延びてしまうことになります。この情報
を使ってデジタルの情報のなかでなにかしようというのがデジタル
フィルターです。内部の情報のフーリエ分解を考えると、減少したとはいえ
サンプリングノイズがあらわにのこっていて3倍波、5倍波などの
成分を持っていることになります。これは補間の方法が不完全だから
残ると思って良いでしょう。元の信号が20kHzまでしか持っていないのに
なかでそれ以上の周波数成分を持ってしまうのはまずいです。
これをそのままDACに食わせるのはもっとまずいでしょう。そこで
デジタルの情報のまま周波数カットをやってしまうのがデジタルフィルター
です。
原理はちょっとやっかいです。デジタル値は
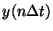 の時間分布
を持っていると考えられます。ここで
の時間分布
を持っていると考えられます。ここで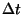 は内部のサンプリング時間
ユニットです。こいつを
は内部のサンプリング時間
ユニットです。こいつを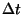 は送らせて入力にK倍して足し合わせる
事を考えます。一発、△関数の入力があるとK>1だと出力は再現なく増加し、
K=1ならなら一定値、K<1のときクロックカウントnに応じてKnで
減少する出力が得られます。従うべき漸化式は
は送らせて入力にK倍して足し合わせる
事を考えます。一発、△関数の入力があるとK>1だと出力は再現なく増加し、
K=1ならなら一定値、K<1のときクロックカウントnに応じてKnで
減少する出力が得られます。従うべき漸化式は
です。ここでxは入力、yは出力です。これに正弦波
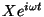 を入れてみると
を入れてみると
なる応答関数を得ます。
従ってこれを通すとなんらかの周波数依存性と位相の回転が
起ります(フィルター作用)。あきらかにこれは周期関数です。
振幅は
で与えられ振幅の最大値は
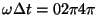 …で与えられ
1/(1-K)で、振幅の最小値は
…で与えられ
1/(1-K)で、振幅の最小値は
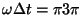 …で与えられ
1/(1+K)です。最小値は標本化周波数の半分のところででますから
それ以下ではローパスフィルターとして機能することになります。
こまったことに高い周波数成分に折り返しが出ることになります。
K=0.5とすると最大値は2で最小値は0.5になりますが、
K=0.8とすると最大値は5で最小値は0.55になります。
今8倍オーバーサンプリングを考えてますから、最小値は4倍の周波数
で得られます。欲しい特性は20kHzまでフラットでそこから
急峻に落ちるものです。この簡単な例ではなかなかうまくは行きませんが
低域フィルターとしては見事に動作してなんとか当初の目的を
達成します。ポイントは4倍周波数まででゆっくり落ちるアナログフィルター
を作ってやれば、サンプリングノイズが簡単に低減できるようになった
ということです。
…で与えられ
1/(1+K)です。最小値は標本化周波数の半分のところででますから
それ以下ではローパスフィルターとして機能することになります。
こまったことに高い周波数成分に折り返しが出ることになります。
K=0.5とすると最大値は2で最小値は0.5になりますが、
K=0.8とすると最大値は5で最小値は0.55になります。
今8倍オーバーサンプリングを考えてますから、最小値は4倍の周波数
で得られます。欲しい特性は20kHzまでフラットでそこから
急峻に落ちるものです。この簡単な例ではなかなかうまくは行きませんが
低域フィルターとしては見事に動作してなんとか当初の目的を
達成します。ポイントは4倍周波数まででゆっくり落ちるアナログフィルター
を作ってやれば、サンプリングノイズが簡単に低減できるようになった
ということです。



Next: 演算・記憶・インターフェイス
Up: デジタル回路との入出力
Previous: サンプル&ホールド回路とサンプリング定理
2000-02-20
![]() の時間分布
を持っていると考えられます。ここで
の時間分布
を持っていると考えられます。ここで![]() は内部のサンプリング時間
ユニットです。こいつを
は内部のサンプリング時間
ユニットです。こいつを![]() は送らせて入力にK倍して足し合わせる
事を考えます。一発、△関数の入力があるとK>1だと出力は再現なく増加し、
K=1ならなら一定値、K<1のときクロックカウントnに応じてKnで
減少する出力が得られます。従うべき漸化式は
は送らせて入力にK倍して足し合わせる
事を考えます。一発、△関数の入力があるとK>1だと出力は再現なく増加し、
K=1ならなら一定値、K<1のときクロックカウントnに応じてKnで
減少する出力が得られます。従うべき漸化式は