四重極磁石による19Neの偏極へ
お勉強へ
作成日:2002年11月 2日 土曜日
四重極磁石による19Neの偏極のシミュレーション結果の解釈
◎グラフを見たらわかること
●実現の可能性が高そうな条件(1)[(1-b),(1-c)]でもある程度分離できる。
●温度を下げた場合(4)[(4-b),(4-c)]はかなり分離される →冷却装置を作るのは大変そう…。
●スリットまでの距離を長くしたり(3)[(3-b),(3-c)]、スリットまでの距離を長くしたり(2)[(2-b),(2-c)]すると(1)のときより分離されるているようだ。
◎得られる偏極率
平行スピンと反平行スピンとが完全に分離されていおらず、ビームの中心付近に局在していて、偏極率Pを厳密にP=1にするのは大変である。
しかし、(1)の場合でも、(1-c)に書いてある数値より、
P=+0.5からP=+1.0の領域に入り口を開けておけば、
反平行の粒子が 3278 + 43201 = 46479個入ってしまうが、
平行の粒子は 122137 + 174131 = 296268個入るので、
合わせると偏極率PはP = (296268 - 46479) / (296268 + 46479) = 73%となる。
同じく(1)で、P=-0.5からP=-1.0の領域に入り口を開けておけば、
平行の粒子が 22414 + 2408 = 24822個入るが、
反平行の粒子が 110865 + 164262 = 275127個入るので、
偏極率はP = (24822 - 275127) / (24822 + 275127) = 83%となる。
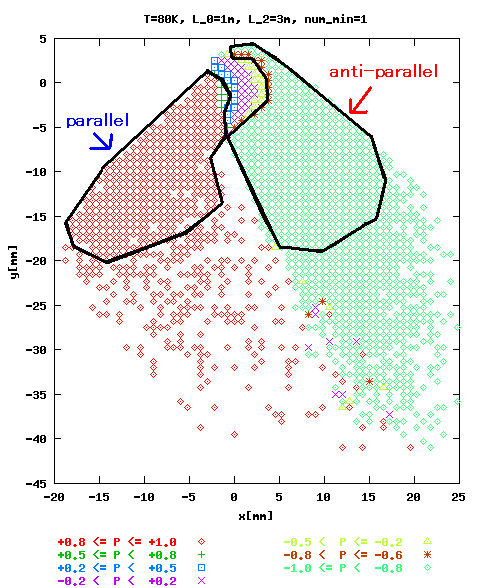
図:入り口の開け方 条件(1)のとき
入射粒子数は各々1,000,000個であるから、偏極率測定に使えるのは
・平行の場合では、入るのが342747(= 296268 + 46479)個で、
正味のスピンが平行な粒子は249789(= 296268 - 46479)個であるから、およそ30%が関与していると言うことができる。
・反平行の場合は、入るのが299949(= 24822 + 275127)個で、
正味のスピンが反平行な粒子は250305(= 275127 - 24822)個であるから、25〜30%が関与していると言うことができる。
主に平行スピンを対象にした検出器と、主に反平行スピンを対象にした検出器を用意して、独立に同時計測すれば、磁石に入射した粒子のうちの約 (30% + 30%) /2 = 30%が偏極率測定に用いられ(減偏極や、測定器から出て行ってしまうことや、検出漏れなどを無視すると)、70%から80%の偏極率が得られることになる。
非対称度因子Aが19NeではA19Ne=-0.036(?)と小さいので、そんなにPの精度が得られないかもしれないから、高偏極度を狙わずに、数を稼いだほうがいいと思う。
同じく、
P=+0.5からP=+1.0の領域と、
P=-0.5からP=-1.0の領域に入り口を開けておくとして
(2)(2-c)、(3)(3-c)、(4)(4-c)の場合でも同じ計算をすると
| 条件 | 平行 | 反平行 | 差し引き | 合計数 | 偏極率P |
| (1) 平行 | 296268 | 46479 | 249789 | 342747 | 73%
|
| (1)反平行 | 24822 | 275127 | 250305 | 299949 | 83%
|
| (2) 平行 | 511473 | 50639 | 460834 | 562112 | 82% |
| (2)反平行 | 37815 | 501533 | 463718 | 539348 | 86%
|
| (3) 平行 | 304445 | 36405 | 268040 | 340850 | 79% |
| (3)反平行 | 27438 | 305957 | 278519 | 333395 | 84%
|
| (4) 平行 | 707379 | 51774 | 655605 | 759153 | 86% |
| (4)反平行 | 30055 | 660306 | 630251 | 690361 | 91% |
◎長さや温度はどうするのがいいか?
1.装置の関係上、冷却すること(4)はあきらめて、液体窒素温度で頑張るとすると、選択肢は「スリット間の距離L0と飛ばす距離L2を増やす」しかない。(それもないかもしれない)
2.19Neの検出はセルの中に入射させて、その中で滞留させるのが良いと考えられる。
3.セルに入れるには入口が必要である。
4.入口が大きければ、出ていく確率も増えるであろう。
5.減偏極のことを無視すれば、滞留時間は長い方が良い。
6.そのためには測定セルへ入口が小さい方が良い。
7.ビームの分布が広がっていないほうが良い。
8.平均自由行程が短い(真空が悪い)ときには、距離が長くなればなるほどビームが散乱される確率が大きくなる。
9.距離が長いほどスリットや検出器の入り口の設定が大変である。
10.高偏極率を狙わないのであれば、上のテーブルの数値からすると、(1)と(3)であまり差は無い。
よって、(3)の場合(10m飛ばす)は大変なだけだろう。やめよう。
●スリット間の距離L0の2乗に反比例して立体角(ビームの数∝立体角)は減少するので、あまり長くしたくないから、
ビームの発散とビームの数の関係でちょうど良いL0を選べば良いだろう。
