


Next: ミラー効果を止めた高周波増幅器,ビデオアンプ
Up: 負帰還と回路の周波数域特性(発振してこまるダメアンプとは)
Previous: 実際の増幅回路の周波数特性
この場合の裸利得は
Av=Adc/(1+if/fc)=GB/(if+fc)
になります。ここでAdcは直流ゲイン、fは周波数、fcは遮断周波数です。
非反転アンプになるように負帰還をかけるた場合、
ですから
で負帰還によってゲインを低下させた分だけ高周波特性が延びていくことになります。
また、
G(f=0)fc'=Adcfcとどう使ってもGB積は一定になることも分かります。
反転増幅器の場合も同様に
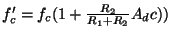 で
で
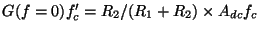 です。
です。
いいことずくめのように見えますが、
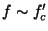 での負帰還量はどうなっているのでしょう。
裸のゲインは
での負帰還量はどうなっているのでしょう。
裸のゲインは
Av=Adc/(1+if/fc)
で、f>>fcで位相は90度まわり、振幅は
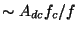 です。
帰還後の振幅は正相増幅の場合の振幅もほぼ、
です。
帰還後の振幅は正相増幅の場合の振幅もほぼ、
になります。位相の回りがからまってむずかしいですがほぼ帰還がなくなって
いることがわかります。
従ってこの点では負帰還のよいところはすべて消失します。すなわち歪みも量は増え
増幅度の安定化も効かないことになります。今裸のゲインが6dB/octと考えているので
これでも発振しませんが、普通の増幅器ではこの辺りの処理がむずかしく発振する
おおきな要因になります。従って広帯域の増幅器は発振しやすいものです。
発振をとめるにはポイントにコンデンサー一発、で済むことが多いです。
結局
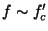 あたりでの位相関係をきれいにしてやるわけです。
帯域をあまり制限してしまわないように入れるのがポイントになります。
あたりでの位相関係をきれいにしてやるわけです。
帯域をあまり制限してしまわないように入れるのがポイントになります。



Next: ミラー効果を止めた高周波増幅器,ビデオアンプ
Up: 負帰還と回路の周波数域特性(発振してこまるダメアンプとは)
Previous: 実際の増幅回路の周波数特性
2000-02-20
![]() での負帰還量はどうなっているのでしょう。
裸のゲインは
での負帰還量はどうなっているのでしょう。
裸のゲインは