Two Body Relativistic Kinematics

Calculation

$m_1(m_2, m_3)m_4$ を考える.

メトリックは,

$$\mqty( \dmat{ 1, -1, -1, -1 } )$$

重心系の速度を $\beta_G$ とすると, Lorentz Boost によって, 次のように変換される.

$$\mqty( \gamma_G & - \beta_G \gamma_G \\ - \beta_G \gamma_G & \gamma_G ) \mqty( E_1^\mathrm{(lab)} \\ p_1^\mathrm{(lab)} )$$ $$\mqty( \gamma_G & - \beta_G \gamma_G \\ - \beta_G \gamma_G & \gamma_G ) \mqty( E_2^\mathrm{(lab)} \\ p_2^\mathrm{(lab)} )$$

ところで, $\beta$, $\gamma$ は

$$\gamma^2 - \beta^2\gamma^2 = 1$$

を満たすので, この変換は

$$\cosh \chi = \gamma,\quad \sinh \chi = \beta \gamma.$$

として,

$$\mqty( \cosh \chi & - \sinh \chi \\ - \sinh \chi & \cosh \chi )$$

とも表せる. SkiSicknessの説明では, これが使われている.

重心系では, $p_1^\mathrm{(CM)} + p_2^\mathrm{(CM)} = 0$ より,

$$\beta_G = \frac{ p_1^\mathrm{(lab)} + p_2^\mathrm{(lab)} }{ E_1^\mathrm{(lab)} + E_2^\mathrm{(lab)} }, \quad \gamma_G = \frac{1}{\sqrt{1-\beta_G^2}} .$$

Mandelstam 変数 $s$ (重心系のエネルギーに相当) はローレンツ不変で,

$$s = (p_1 + p_2)^2 = (E_1 + E_2)^2 - (p_1 + p_2)^2$$

実験室系で入射粒子2の運動エネルギーを $T$, 標的粒子1が静止しているとすると,

$$s = (m_1 + m_2 + T)^2 - p_2^{\mathrm{(lab)}2} = (m_1 + m_2 + T)^2 - \qty( (m_2 + T)^2 - m_2^2 ) = (m_1 + m_2)^2 + 2m_1T$$

$s$ は, ローレンツ不変なので,

$$s = \qty( E_1^\mathrm{(CM)} + E_2^\mathrm{(CM)} )^2 - \qty(p_1^\mathrm{(CM)} + p_2^\mathrm{(CM)})^2 = \qty( \sqrt{ m_1^2 + p_1^{\mathrm{(CM)}2} } + \sqrt{ m_2^2 + p_1^{\mathrm{(CM)}2} } )^2$$

これを変形して,

$$2 \sqrt{ m_1^2 + p_1^{\mathrm{(CM)}2} } \sqrt{ m_2^2 + p_1^{\mathrm{(CM)}2} } = m_1^2 + m_2^2 + 2 p_1^{\mathrm{(CM)}2} -s$$ $$4 m_1^2m_2^2 + 4 (m_1^2 + m_2^2) p_1^{\mathrm{(CM)}2} + 4 p_1^{\mathrm{(CM)}4} = (m_1^2 + m_2^2)^2 + 4 (m_1^2 + m_2^2) p_1^{\mathrm{(CM)}2} + 4 p_1^{\mathrm{(CM)}4} + s^2 - 2 s \qty( m_1^2 + m_2^2 + 2 p_1^{\mathrm{(CM)}2})$$ $$4 m_1^2m_2^2 = (m_1^2 + m_2^2)^2 + s^2 - 2 s \qty( m_1^2 + m_2^2 + 2 p_1^{\mathrm{(CM)}2})$$ $$m_1^4 + m_2^4 - 2m_1^2m_2^2 + s^2 - 2 s \qty( m_1^2 + m_2^2 + 2 p_1^{\mathrm{(CM)}2}) = 0$$ $$4 s p_1^{\mathrm{(CM)}2} + 2 (m_1^2 + m_2^2)^2 - s^2 - (m_1^2 - m_2^2)^2 = 0$$ $$\begin{align*} p_1^{\mathrm{(CM)}2} &= \frac{ (m_1^2 - m_2^2)^2 + s^2 -2s (m_1^2 + m_2^2) }{ 4s }\\ &= \frac{ \qty{ s - \qty(m_1^2 + m_2^2)^2 }^2 - 4 m_1^2 m_2^2 }{ 4s } \end{align*}$$ $$p_1^{\mathrm{(CM)}} = \sqrt{ \frac{ \qty{ s - \qty(m_1^2 + m_2^2)^2 }^2 - 4 m_1^2 m_2^2 }{ 4s } }$$

を得る.

$$E_1^{\mathrm{(CM)}} = m_1 \gamma_G = m_1 \cosh \chi = \sqrt{m_1^2 + p_1^{\mathrm{(CM)}2} }$$ $$p_1^{\mathrm{(CM)}} = m_1 \beta_G \gamma_G = m_1 \sinh \chi = p_1^{\mathrm{(CM)}}$$

より,

$$\cosh \chi = \frac{\sqrt{m_1^2 + p_1^{\mathrm{(CM)}2}}}{m_1}, \quad \sinh \chi = \frac{p_1^{\mathrm{(CM)}}}{m_1}.$$

また, $\sinh \chi + \cosh \chi = \exp \chi$ より, $\chi$ は

$$\chi = \ln\qty( \frac{ p_1^{\mathrm{(CM)}} + \sqrt{m_1^2 + p_1^{\mathrm{(CM)}2}} }{m_1} )$$

と表せる.

$s$ は保存され, 重心系では $p_3^{\mathrm{(CM)}} + p_4^{\mathrm{(CM)}} = 0$ より,

$$\begin{align*} s &= \qty(E_3^{\mathrm{(CM)}} + E_4^{\mathrm{(CM)}})^2 \\ &= \qty( \sqrt{ m_3^2 + p_3^{\mathrm{(CM)}2} } + \sqrt{ m_4^2 + p_4^{\mathrm{(CM)}2} } )^2 \end{align*}$$

上と同じようにして,

$$p_3^{\mathrm{(CM)}} = \sqrt{ \frac{ \qty{ s - \qty(m_3^2 + m_4^2)^2 }^2 - 4 m_3^2 m_4^2 }{ 4s } }$$

を得る.

したがって, 重心系での粒子3,4のエネルギー $E_3^{\mathrm{(CM)}}$, $E_4^{\mathrm{(CM)}}$ は

$$\begin{align*} E_3^{\mathrm{(CM)}2} &= m_3^2 + p_3^{\mathrm{(CM)}2}\\ &= m_3^2 + \frac{ \qty{s - \qty(m_3^2 + m_4^2)^2}^2- 4 m_3^2 m_4^2 }{4s}\\ &= \frac{ \qty{s + \qty(m_3^2 - m_4^2)^2}^2 }{ 4s } \end{align*}$$ $$E_3^{\mathrm{(CM)}} = \frac{ s + \qty(m_3^2 - m_4^2)^2 }{ 2 \sqrt{s} }$$

$E_3^{\mathrm{(CM)}} + E_4^{\mathrm{(CM)}} = \sqrt{s}$ より,

$$E_4^{\mathrm{(CM)}} = \frac{ s - \qty(m_3^2 - m_4^2)^2 }{ 2 \sqrt{s} }$$

重心系での粒子3,4の4元運動量:

$$\mqty( E_3^{\mathrm{(CM)}} \\ p_3^{\mathrm{(CM)}} ), \quad \mqty( E_4^{\mathrm{(CM)}} \\ - p_3^{\mathrm{(CM)}} ).$$

をローレンツ逆変換して, 実験室系に戻す.

$$\mqty( \gamma_G & \beta_G \gamma_G \\ \beta_G \gamma_G & \gamma_G ) \mqty( E_3^{\mathrm{(CM)}} \\ p_3^{\mathrm{(CM)}} \cos \theta^{\mathrm{(CM)}} ) = \mqty( \gamma_G E_3^{\mathrm{(CM)}} + \beta_G \gamma_G p_3^{\mathrm{(CM)}} \cos \theta^{\mathrm{(CM)}} \\ \beta_G \gamma_G E_3^{\mathrm{(CM)}} + \gamma_G p_3^{\mathrm{(CM)}} \cos \theta^{\mathrm{(CM)}} ) = \mqty( E_3^{\mathrm{(lab)}} \\ p_3^{\mathrm{(lab)}} \cos \theta_3^{\mathrm{(lab)}} )$$ $$\mqty( \gamma_G & \beta_G \gamma_G \\ \beta_G \gamma_G & \gamma_G ) \mqty( E_4^{\mathrm{(CM)}} \\ - p_3^{\mathrm{(CM)}} \cos \theta_3^{\mathrm{(CM)}} ) = \mqty( \gamma_G E_4^{\mathrm{(CM)}} - \beta_G \gamma_G p_3^{\mathrm{(CM)}} \cos \theta^{\mathrm{(CM)}} \\ \beta_G \gamma_G E_4^{\mathrm{(CM)}} - \gamma_G p_3^{\mathrm{(CM)}} \cos \theta^{\mathrm{(CM)}} ) = \mqty( E_4^{\mathrm{(lab)}} \\ p_4^{\mathrm{(lab)}} \cos \theta_4^{\mathrm{(lab)}} )$$

垂直な成分は変わらないので,

$$\begin{align*} p_3^{\mathrm{(CM)}} \sin \theta^{\mathrm{(CM)}} &= p_3^{\mathrm{(lab)}} \sin \theta_3^{\mathrm{(lab)}} \\ p_4^{\mathrm{(CM)}} \sin \theta^{\mathrm{(CM)}} &= p_4^{\mathrm{(lab)}} \sin \theta_4^{\mathrm{(lab)}} \\ \end{align*}$$

以上より, 実験室系での運動エネルギーは,

$$T_3^{\mathrm{(lab)}} = E_3^{\mathrm{(lab)}} - m_3, \quad T_4^{\mathrm{(lab)}} = E_4^{\mathrm{(lab)}} - m_4.$$

実験室系での運動量は,

$$\begin{align*} p_3^{\mathrm{(lab)}2} &= \qty( p_3^{\mathrm{(lab)}} \sin \theta_3^{\mathrm{(lab)}} )^2 + \qty( p_3^{\mathrm{(lab)}} \cos \theta_3^{\mathrm{(lab)}} )^2 ,\\ p_4^{\mathrm{(lab)}2} &= \qty( p_4^{\mathrm{(lab)}} \sin \theta_4^{\mathrm{(lab)}} )^2 + \qty( p_4^{\mathrm{(lab)}} \cos \theta_4^{\mathrm{(lab)}} )^2 . \end{align*}$$

実験室系での角度は,

$$\begin{align*} \theta_3^{\mathrm{(lab)}} &= \arctan\qty( \frac{ p_3^{\mathrm{(lab)}} \sin \theta_3^{\mathrm{(lab)}} }{ p_3^{\mathrm{(lab)}} \cos \theta_3^{\mathrm{(lab)}} } ) = \arctan\qty( \frac{ p_3^{\mathrm{(CM)}} \sin \theta_3^{\mathrm{(CM)}} }{ \beta_G \gamma_G E_3^{\mathrm{(CM)}} + \gamma_G p_3^{\mathrm{(CM)}} \cos \theta^{\mathrm{(CM)}} } ) \\ \theta_4^{\mathrm{(lab)}} &= \arctan\qty( \frac{ p_4^{\mathrm{(lab)}} \sin \theta_4^{\mathrm{(lab)}} }{ p_4^{\mathrm{(lab)}} \cos \theta_4^{\mathrm{(lab)}} } ) = \arctan\qty( \frac{ p_3^{\mathrm{(CM)}} \sin \theta_3^{\mathrm{(CM)}} }{ \beta_G \gamma_G E_4^{\mathrm{(CM)}} - \gamma_G p_3^{\mathrm{(CM)}} \cos \theta^{\mathrm{(CM)}} } ) \end{align*}$$

となる.

$$\tan \theta_3^{\mathrm{(lab)}} = \frac{ p_3^{\mathrm{(lab)}} \sin \theta_3^{\mathrm{(lab)}} }{ p_3^{\mathrm{(lab)}} \cos \theta_3^{\mathrm{(lab)}} } = \frac{ p_3^{\mathrm{(CM)}} \sin \theta_3^{\mathrm{(CM)}} }{ \gamma p_3^{\mathrm{(CM)}} \cos \theta_3^{\mathrm{(CM)}} + \beta \gamma E_3^{\mathrm{(CM)}} }$$ $$\gamma \tan \theta_3^{\mathrm{(lab)}} \cos \theta_3^{\mathrm{(CM)}} - \sin \theta_3^{\mathrm{(CM)}} = - \frac{ \beta \gamma E_3^{\mathrm{(CM)}} \tan \theta_3^{\mathrm{(lab)}} }{ p_3^{\mathrm{(CM)}} }$$ $$\cos \qty( \theta_3^{\mathrm{(CM)}} + \alpha) = - \frac{ \beta \gamma E_3^{\mathrm{(CM)}} \tan \theta_3^{\mathrm{(lab)}} }{ p_3^{\mathrm{(CM)}} \sqrt{ \gamma^2 \tan^2 \theta_3^{\mathrm{(lab)}} + 1 } }$$ $$\tan \alpha = \frac{1}{\gamma \tan \theta_3^{\mathrm{(lab)}}} \quad (0 < \alpha < \pi/2)$$ $$\theta_3^{\mathrm{(CM)}} + \alpha = \arccos\qty( - \frac{ \beta \gamma E_3^{\mathrm{(CM)}} \tan \theta_3^{\mathrm{(lab)}} }{ p_3^{\mathrm{(CM)}} \sqrt{ \gamma^2 \tan^2 \theta_3^{\mathrm{(lab)}} + 1 } } )$$

同様に

$$\theta_4^{\mathrm{(CM)}} - \alpha = \arccos\qty( \frac{ \beta \gamma E_4^{\mathrm{(CM)}} \tan \theta_4^{\mathrm{(lab)}} }{ p_3^{\mathrm{(CM)}} \sqrt{ \gamma^2 \tan^2 \theta_4^{\mathrm{(lab)}} + 1 } } )$$ $$\tan \alpha = \frac{1}{\gamma \tan \theta_4^{\mathrm{(lab)}}} \quad (0 < \alpha < \pi/2)$$

Program

Python で計算するスクリプトを書いてみた.

relkin.py

import numpy as np

class kinema():
    def __init__(self, m1, m2, m3, m4, num=1000):
        self.m1 = m1
        self.m2 = m2
        self.m3 = m3
        self.m4 = m4
        self.theta_cm = np.linspace(1e-5, np.pi-1e-5, num)
        self.p_cm = 0.0
        self.T3_cm = 0.0
        self.T4_cm = 0.0
        self.theta3_lab = np.zeros(num)
        self.theta4_lab = np.zeros(num)
        self.T3_lab = np.zeros(num)
        self.T4_lab = np.zeros(num)
        self.p3_lab = np.zeros(num)
        self.p4_lab = np.zeros(num)
        self.beta3_lab = np.zeros(num)
        self.beta4_lab = np.zeros(num)

    def calc(self, T):
        m1 = self.m1
        m2 = self.m2
        m3 = self.m3
        m4 = self.m4
        theta_cm = self.theta_cm
        
        sq = lambda x : np.power(x,2)

        # mandelstam variable s
        s = sq(m1 + m2) + 2*m1*T
        # Momentum in the CM
        pcm12 = np.sqrt( (sq(s - sq(m1) - sq(m2)) - 4*sq(m1)*sq(m2)) / (4*s) )
        gamma = np.sqrt(sq(m1) + sq(pcm12)) / m1 # coshX
        beta_gamma = pcm12 / m1 # sinhX

        # Energy of particles 3 & 4 in CM
        E3_cm = ( s + (sq(m3) - sq(m4)) ) / (2 * np.sqrt(s))
        E4_cm = ( s - (sq(m3) - sq(m4)) ) / (2 * np.sqrt(s))
        
        # Kinetic energy of particles 3 & 4 in CM
        self.T3_cm = E3_cm - m3
        self.T4_cm = E4_cm - m4
        
        # Momentum in the CM
        self.p_cm = np.sqrt( (sq(s - sq(m3) - sq(m4)) - 4*sq(m3)*sq(m4)) / (4*s) )
        p_cm = self.p_cm
        
        # Energy of particles 3 & 4 in Lab
        E3_lab = gamma * E3_cm + beta_gamma * p_cm * np.cos(theta_cm)
        E4_lab = gamma * E4_cm - beta_gamma * p_cm * np.cos(theta_cm)
        
        # Kinetic energy of particles 3 & 4 in Lab
        self.T3_lab = E3_lab - m3
        self.T4_lab = E4_lab - m4
        
        # Momentum in Lab
        p3cos = gamma * p_cm * np.cos(theta_cm) + E3_cm * beta_gamma
        p4cos = - gamma * p_cm * np.cos(theta_cm) + E4_cm * beta_gamma
        p3sin = p_cm * np.sin(theta_cm)
        p4sin = p_cm * np.sin(theta_cm)
        self.p3_lab = np.sqrt(sq(p3cos) + sq(p3sin))
        self.p4_lab = np.sqrt(sq(p4cos) + sq(p4sin))

        # Beta in Lab
        gamma3_lab = E3_lab/m3
        gamma4_lab = E4_lab/m4
        self.beta3_lab = np.sqrt( (sq(gamma3_lab) - 1)/sq(gamma3_lab) )
        self.beta4_lab = np.sqrt( (sq(gamma4_lab) - 1)/sq(gamma4_lab) )

        # Theta in Lab
        self.theta3_lab = np.arctan(p3sin/p3cos)
        self.theta4_lab = np.arctan(p4sin/p4cos)

Example

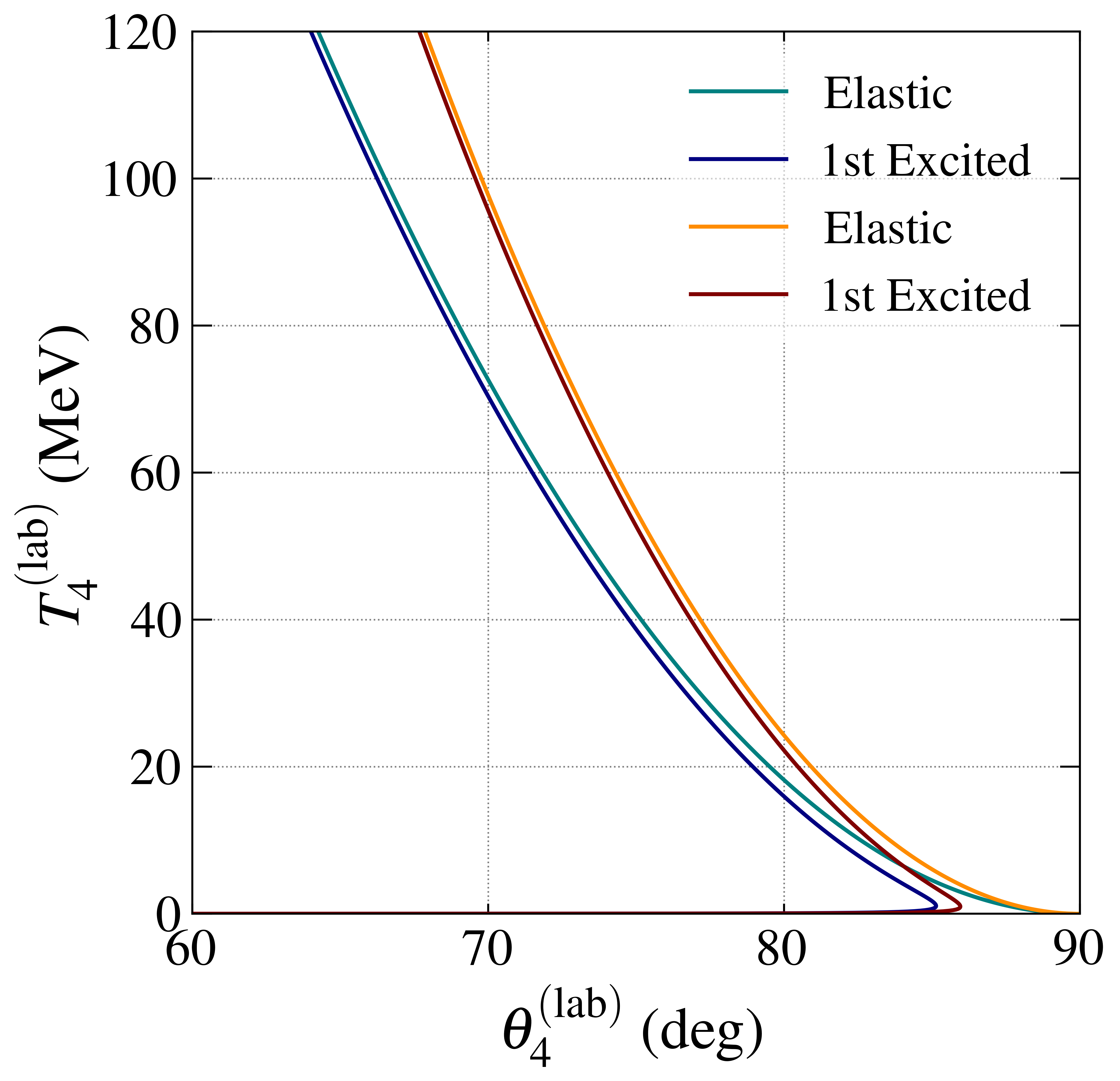
Proton Elastic Scattering from ¹³⁶Xe

p(¹³⁶Xe, ¹³⁶Xe)p (@ 200 & 300 MeV/u) の反跳陽子の実験室系での運動学をプロットする. ついでに ¹³⁶Xe の第一励起状態の運動学もプロットする.

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from relkin import kinema

u = 931.49410372

mass = (
    938.27208943, # MeV
    135.907214484 * u, # MeV
    135.907214484 * u, # MeV
    938.27208943 # MeV
)
xe200 = kinema(*mass)
xe300 = kinema(*mass)

mass_ex = (
    938.27208943, # MeV
    135.907214484 * u, # MeV
    135.907214484 * u + 1.313, # MeV
    938.27208943 # MeV
)

xe200_ex = kinema(*mass_ex)
xe300_ex = kinema(*mass_ex)

xe200.calc(200*136)
xe300.calc(300*136)
xe200_ex.calc(200*136)
xe300_ex.calc(300*136)

plt.figure(0, figsize=(8,8), dpi=600)

plt.plot(
    np.rad2deg(xe200.theta4_lab),
    xe200.T4_lab,
    color="teal",
    label="Elastic",
    lw=2)

plt.plot(
    np.rad2deg(xe200_ex.theta4_lab),
    xe200_ex.T4_lab,
    color="navy",
    label="1st Excited",
    lw=2)

plt.plot(
    np.rad2deg(xe300.theta4_lab),
    xe300.T4_lab,
    color="darkorange",
    label="Elastic",
    lw=2)

plt.plot(
    np.rad2deg(xe300_ex.theta4_lab),
    xe300_ex.T4_lab,
    color="maroon",
    label="1st Excited",
    lw=2)

plt.legend()
plt.xlim(60,90)
plt.ylim(0,120)

Cluster Knockout Reaction

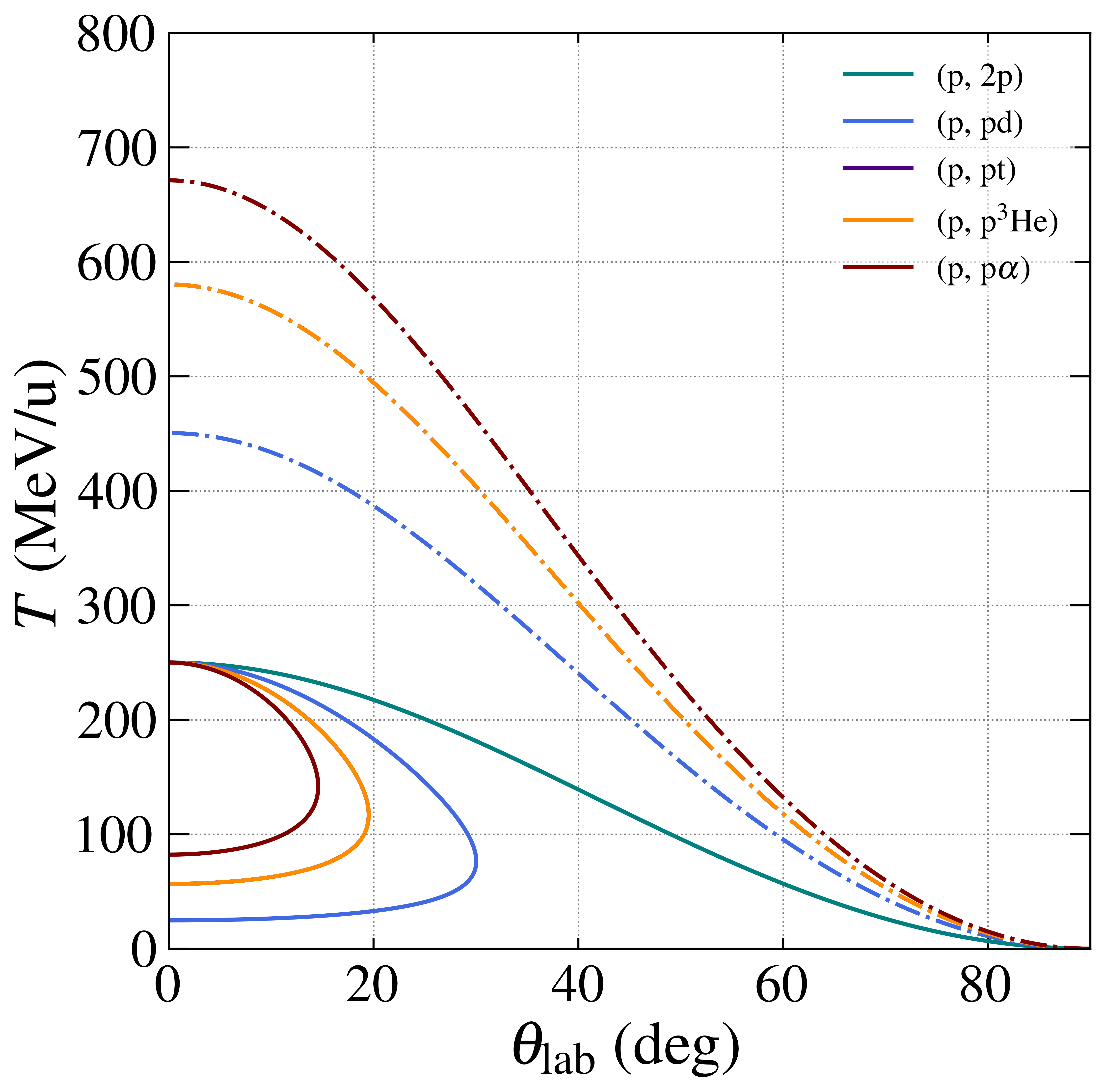
(p,2p), (p,pX)の素過程, p, d, t, ³He, $\alpha$ と p の弾性散乱の運動学をプロットする.

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

from relkin import kinema

# Mass
u = 931.49410372 # MeV
# Z = 1
mp = 1.00782503223 * u
md = 2.01410177812 * u
mt = 3.01604927790 * u
# Z = 2
m3He = 3.01602932007 * u
ma = 4.001506179127 * u

m_p2p = (mp,mp,mp,mp)
m_ppd = (mp,md,md,mp)
m_ppt = (mp,mt,mt,mp)
m_pp3He = (mp,m3He,m3He,mp)
m_ppa = (mp,ma,ma,mp)

kinema_p2p = kinema(*m_p2p)
kinema_ppd = kinema(*m_ppd)
kinema_ppt = kinema(*m_ppt)
kinema_pp3He = kinema(*m_pp3He)
kinema_ppa = kinema(*m_ppa)

kinema_p2p.calc(250)
kinema_ppd.calc(250*2)
kinema_ppt.calc(250*3)
kinema_pp3He.calc(250*3)
kinema_ppa.calc(250*4)

plt.figure(0, figsize=(8,8), dpi=600)

## (p,p2p)
# p
plt.plot(
    np.rad2deg(kinema_p2p.theta4_lab),
    kinema_p2p.T4_lab/1,
    color="teal",
    label=r"(p, 2p)",
    lw=2)


## (p,pd)
# d
plt.plot(
    np.rad2deg(kinema_ppd.theta3_lab),
    kinema_ppd.T3_lab/2,
    color="royalblue",
    label=r"(p, pd)",
    lw=2)
# p
plt.plot(
    np.rad2deg(kinema_ppd.theta4_lab),
    kinema_ppd.T4_lab,
    color="royalblue",
    ls='-.',
    lw=2)


## (p,pt)
# t
plt.plot(
    np.rad2deg(kinema_ppt.theta3_lab),
    kinema_ppt.T3_lab/3,
    color="indigo",
    label=r"(p, pt)",
    lw=2)
# p
plt.plot(
    np.rad2deg(kinema_ppt.theta4_lab),
    kinema_ppt.T4_lab,
    color="indigo",
    ls='-.',
    lw=2)


## (p,p3He)
# 3He
plt.plot(
    np.rad2deg(kinema_pp3He.theta3_lab),
    kinema_pp3He.T3_lab/3,
    color="darkorange",
    label=r"(p, p$^{3}$He)",
    lw=2)
# p
plt.plot(
    np.rad2deg(kinema_ppt.theta4_lab),
    kinema_ppt.T4_lab,
    color="darkorange",
    ls='-.',
    lw=2)


## (p,pa)
# a
plt.plot(
    np.rad2deg(kinema_ppa.theta3_lab),
    kinema_ppa.T3_lab/4,
    color="maroon",
    label=r"(p, p$\alpha$)",
    lw=2)
# p
plt.plot(
    np.rad2deg(kinema_ppa.theta4_lab),
    kinema_ppa.T4_lab,
    color="maroon",
    ls='-.',
    lw=2)

plt.legend()

plt.xlabel(r"$\theta_\mathrm{lab}$ (deg)")
plt.ylabel(r"$T$ (MeV/u)")
plt.xlim(0,90)
plt.ylim(0,800)

References

• https://skisickness.com/2010/04/25/
• http://lambda.phys.tohoku.ac.jp/~miwa9/monte_carlo/kinematics.pdf
• https://pdg.lbl.gov/2023/reviews/kinematics_and_cross_sections.html